Monthly Archives: June 2010

Joel Stein on Edison, NJ : poor taste (needs more curry?)

Posted on by

Joel Stein has an truly atrocious piece in Time magazine, which opens with

I am very much in favor of immigration everywhere in the U.S. except Edison, N.J.

I can see how Stein is sort of trying to be funny, but the whole piece has a stink (like uncooked hing) about it that got Anna up in arms and Mimosa writing:

But really, what bothers me about this piece, why it didn’t strike me as satire, is that it seems to assume that there really is a dominant narrative out there, i.e. that “white” culture is where it’s at. Assimilation is not an option, it’s a requirement for these rude new aliens – but of course, that assimilation is on the dominant narratives terms.

Klein’s response:

Didn’t meant to insult Indians with my column this week. Also stupidly assumed their emails would follow that Gandhi non-violence thing.

Perhaps he thought the emails would also be curry flavo(u)red?

On that note, here is a quote from Amitava Kumar’s Passport Photos, which I am enjoying right now:

If the word ‘curry’ doesn’t have a stable referent or a fixed origin, how can its changing use by postcolonials be seen as a sign of resistance?

unfair labor practices and the UC postdoc union

Posted on by

The University of California (UC) postdocs are trying to form a union to (among other things) get a uniform contract, workplace protections, etc. The UC administration has (true to form) stalled on giving information for negotiations. Congressman George Miller sent a rather strongly worded letter to Yudof after a congressional hearing was was held in Berkeley. More recently the union filed an unfair labor practices charge with the California Public Employment Relations Board.

Beryl Benderly has been covering this story for Science Magazine – links to some of her posts are above.

Found art

Posted on by

As I went for a walk this morning I passed the Bank of America on University – usually a pretty deserted stretch but today brightly colored by the contents of an upended Monopoly set, bright yellow Community Chest cards and 10 dollar bills scattered on the sidewalk. In front of the doors, face up, a salmon “Get out of jail free.” A homeless man reaches down for the top hat.

UC Libraries vs. the Nature Publishing Group

Posted on by

Earlier this month, a letter was circulated to the UC Faculty regarding the Nature Publishing Group (NPG)’s proposal to increase the licensing fees for online access by 400%, which is pretty dramatic given a) the high cost of the subscription in the first place and b) the fact that library budgets are going down. There was a suggestion of a boycott.

NPG felt like they had been misrepresented, and issued a press statement saying “you guys are a bunch of whiners, our stuff is the best, and 7% price hikes per year is totally reasonable.” Furthermore, they said “you guys have been getting a crazy good deal for way too long anyhow and its time you paid your fair share.” I suppose behaving like complete jerks is an ok way to react when you are trying to sell somebody something, especially something that is made up of stuff written by your potential buyers. I wonder what their profit margins are like.

The University of California responded, pointing out that 7% increases, compounded, starts getting out of hand pretty fast. “Plainly put, UC Faculty do not
think that their libraries should have to pay exorbitant and unreasonable fees to get access to their own work.”

Looks like PLoS better start rolling out some new titles!

More info can be found at the OSC website, which oddly doesn’t say what OSC stands for.

ISIT 2010 : talks about adversaries

Posted on by

My thesis work was about a particular adversarial model from Shannon theory (the arbitrarily varying channel), but I am more broadly interested in how adversarial assumptions can be used to capture uncertainty in modeling or add an element of robustness to designs. I’m not wedded to the AVC, so I like going to see other works which try to address these issues. Among the talks I saw at ISIT, these three captured different aspects of these models.

POLYTOPE CODES AGAINST ADVERSARIES IN NETWORKS
(Oliver Kosut; Cornell University, Lang Tong; Cornell University, David Tse; University of California at Berkeley)
This talk used as an example the “cockroach network,” named thusly because it “does not look like a butterfly.” That line got a lot of laughs. In this model a subset of nodes in the network are controlled by an adversary, who can introduce errors. They show that by using a certain structured code called a polytope code, together with some checking and filtering by internal nodes, the adversaries can be detected/avoided. For some networks (planar) they can show that their code achieves the cut-set bound. The key to the codes working is making any adversarial action result in certain tuples of random variables becoming atypical and hence detectable.

JAMMING GAMES FOR POWER CONTROLLED MEDIUM ACCESS WITH DYNAMIC TRAFFIC
(Yalin Sagduyu; Intelligent Automation Inc./University of Maryland, Randall Berry; Northwestern University, Anthony Ephremides; University of Maryland)
This uses adversarial modeling (in the form of game theory) to model how users in a multiaccess setting contend for resources in the presence of jammers. In the AVC context, La and Anantharam proved some early results on these models. Here the extension was that the jammer(s) do not know whether or not the transmitter will be sending anything in a given slot (hence dynamic traffic). In the case with a single transmitter and a single jammer, the model is that the transmitter has to minimize its energy subject to an average rate constraint (packets are coming in at a certain rate to the transmitter and have to passed along). The jammer has a power constraint and wants the transmitter to maximize its energy. It turns out the that if the jammer doesn’t know the queue state of the transmitter, then it has to be on all the time. They have more complicated extensions to multi-transmitter scenarios.

ON THE DETERMINISTIC CODE CAPACITY REGION OF AN ARBITRARILY VARYING MULTIPLE-ACCESS CHANNEL UNDER LIST DECODING
(Sirin Nitinawarat; University of Maryland)
Sirin talked in the session I was in. For point-to-point AVCs under average error, there is a finite list size L called the symmetrizability of the channel such that for list-decoding with list sizes \le L the capacity is 0 and for larger list sizes the capacity is the randomized coding capacity of the AVC. This work extended this to the multiaccess setting, which is a particularly tricky beast since the capacity region itself is nonconvex. He showed that there is a U such that the capacity region has empty interior if the list size is \le U and that for list sizes \ge (U+1)^2 you get back the randomized coding capacity. What is open is whether the list sizes for the two users can be different, so that this gap could be closed, but that problem seems pretty hard to tackle.

CODING AGAINST DELAYED ADVERSARIES
(Bikash Kumar Dey; Indian Institute of Technology, Bombay, Sidharth Jaggi; Chinese University of Hong Kong, Michael Langberg; Open University of Israel, Anand Sarwate; University of California, San Diego)
I guess I’ll be shameless and blog about my own paper — we looked at an adversarial setting where the adversary gets to see the transmitted symbols after a delay. We assumed that the delay grew linearly with the blocklength, so that the transmitter gets to act at time i based on x_1, x_2, \ldots, x_{i - \Delta n}, where n is the blocklength and \Delta is the delay parameter. Suppose everything is binary and the adversary gets to flip a total of pn bits of the codeword but has to see it causally with delay \Delta n. If \Delta = 1 the adversary sees nothing and the average-error capacity is 1 - h(p) bits. If \Delta = 0 the adversary can do a lot worse and the capacity is 1 - 4p bits. What we show is that for any \Delta > 0 we go back to 1 - h(p) bits (and there was much rejoicing). The key is allowing the encoder to randomize, which effectively prevents the adversary from learning anything. Luckily, the decoder can still figure out what is going on (as long as there is some additional slack in the rate), even though it does not share common randomness with the encoder.

Explicit constructions of Expanders and LDPC codes

Posted on by
After seeing Nisim’s ISIT talk on LP Decoding of Regular LDPC Codes in Memoryless Channels, I remembered one issue that has been puzzling me for a while: if there are any explicit constructions of LDPC codes that have a provable nonzero threshold (for block-error probability, hence excluding density evolution arguments) i.e. correct a constant fraction of bit-flipping errors (other channels would be harder)– under any efficient decoder.
The question seems trivial: As is well-known,  a random (d_v,d_c) regular graph will be a very high quality expander (for very small sets) and therefore a (very small) constant fraction of bit-flipping errors can be corrected by Sipser & Spielman‘s bit flipping algorithm.
Also the work by Feldman et al. LP decoding corrects a constant fraction of errors establishes correction of an adversarial set of bit-flipping errors for expander graphs under LP decoding.
But here is the catch: sure, a random graph is a good expander with high probability, but how do we check if a given graph is a good expander?
The key of course is my definition of explicit construction: I mean an algorithm that terminates in polynomial time and gives me a code that certifiably works (and I think this is relevant to practice, since at the end of the day I have to use one fixed code). The only efficient way that I know to check expansion involves spectral methods ( This is from Modern Coding theory by Richardson & Urbanke) : If we have a (d_v,d_c) regular bipartite graph with n variable nodes and \frac{d_v}{ d_c} n check nodes, if we take H to be the incidence matrix of the bipartite graph (the parity check matrix of the code), we can form H^T H and look at its eigenvalues
\lambda_1 \geq \lambda_2,\geq \lambda_3 \cdots and Tanner’s spectral bound on expansion is that expansion \gamma is greater than
\gamma(\alpha) \geq \frac{ d_v}{(d_v d_c - \lambda_2) \alpha + \lambda_2} for any size of expanding sets $\alpha$. Unfortunately this bound cannot certify expansion for any \gamma >1/2, which is exactly the point where it starts being useful for coding theory. Perhaps there are stronger spectral bounds that could establish more expansion, the book Spectral Graph Theory by Fan Chung Graham contains a lot of material on that point but I have not seen any such applications to coding.
So ok, lets say we do not know how to construct (or certify) that LDPCs have high expansion, how about other graph properties that will guarantee a correctable fraction of errors in polynomial time? This started when I was working with Costas on LP decoding for LDPC codes and we were always (incorrectly) assuming that random regular bipartite graphs will have \log n girth with high probability. When we actually tried to find a proof for this, for example looking at the Modern Coding theory book we find that usual proofs establish a significantly weaker statement: in a random (d_v,d_c) regular graph, if you start from a variable and start expanding the tree, you will not loop around after a constant number of steps with 1/poly(n) probability. This is what is refered to as ‘locally-tree like’. I do not know of any stronger statements but I think it can be easily shown that for any fixed cycle length, the expected number of cycles of that length is constant for regular random graphs.
The breakthrough paper by Arora, Daskalakis and Steurer, ‘Message-Passing Algorithms and Improved LP Decoding‘ establishes that regular LDPCs with \log n girth will correct a constant fraction of random bit-flipping errors whp under LP decoding. But how do we find regular LDPCs with \log n girth ?
After searching a little I found the recent work of Bayati et al.
Generating Random Graphs with Large Girth and Generating random Tanner-graphs with large girth that talk about the related problem of generating a graph with high girth uniformly from all such graphs (and with a given degree distribution) but as far as I understood these constructions cannot guarantee a diameter scaling like \log n (but only any constant diameter). This is of course the relevant practical question but the scaling issue remains.
The only construction that I know is the one found in the appendix of Gallager’s thesis that contains a deterministic algorithm that constructs (d_v,d_c) regular Tanner graphs with \log n girth.
The same question is relevant for compressed sensing when we ask for sparsity in the measurement matrix: All the constructions that I know for sparse measurement matrices (that require the optimal number of measurements under Basis pursuit, e.g. see the survey of Gilbert and Indyk: Sparse Recovery using Sparse Matrices) are constructed from high \gamma>2/3 bipartite expander graphs. But given a fixed measurement matrix how do we certify that it is good and should be implemented in a system?
Of course one can use Message passing algorithms for compressed sensing (by Donoho, Maleki and Montanari) and obtain sparse measurement matrices with very good thresholds but under a different decoding algorithm.
The close connection of compressed sensing (under LP – Basis pursuit decoding) and channel coding (under LP decoding) gives one path for certifiable measurement matrices that are sparse):
1. The Arora, Daskalakis & Steurer paper guarantees that (3,6) regular graphs with \log n girth correct a (quite high– much higher than expansion arguments) constant fraction of errors under LP decoding.
2. Gallager’s thesis appendix contains deterministic constructions of such (3,6) regular sparse matrices.
3. Our connection result establishes that if a matrix corrects a constant fraction of bit flipping errors, the same matrix used as a compressed sensing measurement matrix will recover all sparse signals (of the same support as the bit-flipping errors).
Combining (1)+(2)+(3) we obtain that: for sensing a length n signal with m=n/2  measurements one recovers almost all sparse signals of size up to $0.05 n$ (whp over supports) and the (0,1) measurement matrix has O(n) non-zeros. (see our recent paper )
Conclusion: The Appendix C in Gallager’s thesis contains the best sparse compressed sensing measurement matrices known (under basis pursuit).
Not bad for 1963!


ISIT 2010 : databases

Posted on by

I attended one talk on databases and unfortunately missed the second one, so the writeup I have is based on the paper…

IDENTIFICATION AND LOSSY RECONSTRUCTION IN NOISY DATABASES
(Ertem Tuncel; University of California, Riverside and Deniz Gunduz; Centre Tecnologic de Telecomunicacions de Catalunya)
This was the talk I did attend. The goal was to information-theoritize the notion of compressing databases. You get M i.i.d. individuals with characteristics distributed according to P_X and features Y conditioned on the individuals according to P_{Y | X}. The identification problem is this: given a noisy feature vector Z generated from a particular individual X(i) retrieve the index of the user corresponding to Z. This paper looked at the case where you want to recover a distorted version of Y(i), so they are trading off identification and distortion. The solution is to code Wyner-Zivly, and the result recover the existing results on the identification problem alone as well as the Wyner-Ziv problem.

A THEORY OF UTILITY AND PRIVACY OF DATA SOURCES
Lalitha Sankar; Princeton University, S. Raj Rajagopalan; HP Labs, H. Vincent Poor; Princeton University
This talk I missed, which is all the more sad because I work on this stuff. But I did get to see a version of it at ITA and also at the IPAM workshop on privacy (as a poster). This is again an attempt to information-theoretize the problem of data disclosure: given a database d of n individuals, release a noisy version of this database. In doing so, they assume that each individual has K features and the n rows are generated iid according to some distribution P. So, as they put in the paper, “the primary contribution is demonstrating the equivalence between the database privacy problem and a source coding problem with additional privacy constraints.” The notion of utility is captured by a distortion measure: the encoder maps each database to a string of bits W. A user with side information Z^n can attempt to reconstruct the database using the a lossy source code decoder. The notion of privacy by an equivocation constraint:
\frac{1}{n} H( X^n | W, Z^n) \ge E - \epsilon
They then set about finding the best utility-privacy (= distortion-equivocation) tradeoff. This is a different model than differential privacy, and rests on a number of information-theoretic assumptions that may be relaxed in the future. For example, assuming individuals are i.i.d., that distributions are known, that the side information sequence is known, and so on would give pause to the differential privacy crowd. Much like the epsilon in differential privacy, the equivocation has a meaning but its syntactic effect is hard to parse. I guess this is why syntactic definitions of privacy like k-anonymity are popular — it’s easy to see what they mean “on the ground.”

Secrecy and Security in Distributed Storage

Posted on by

Secure Distributive Storage of Decentralized Source Data: Can Interaction Help?

Salim El Rouayheb, Vinod Prabhakaran and Kannan Ramchandran

Salim presented this work on creating a distributed storage system that also has secrecy. As far as I understood, the model is that there are k distributed sources and they want to create a good erasure code in a network: a data collector who accesses any k out of n storage nodes should be able to recover the data. In addition, one storage node is an eavesdropper who gets access to everything communicated to her. The question is to create a distributed code that also has secrecy (i.e. the eavesdropper learns nothing other than what is contained in the nodes she controls) but minimize the communication in the network.

In the model each storage node has a private key and these keys can be used to provide the desired secrecy. The nodes could use interactive protocols of exchanging keys etc, but the main result of the paper is that this does not reduce the required communication compared to a one-way dissemination scheme.

Security in Distributed Storage Systems by Communicating a Logarithmic Number of Bits

by Theodoros K. Dikaliotis, myself and Tracey Ho,

Ted presented our work on security (error correction) for distributed storage systems. We are looking into the problem of finding if a storage node in an (n,k) system is storing incorrect equations. These could be originating from bit-flipping errors in the storage medium or (more likely) if a malicious node was injecting errors during a previous repair in the storage system.

The model is that we assume a trusted verifier that communicates to the nodes and uses the built in redundancy of the code to find where the errors are located. The first observation is in most distributed storage systems the same code is used multiple times to reduce the overhead from storing the coefficients of the code. Instead of sending all the packets, all the storage nodes can project onto the same vector r and only send the projections. The error detection works since the projected data follows the same (n,k) code which can tolerate up to half the minimum distance adversarial errors (under optimal decoding). The problem is that the vector r is very long, around the same order as the stored data. One way around this is to create a pseudorandom r' using a small seed s, and project on that. All the storage nodes need to share the small seed s and if we use pseudorandom generators that fool linear functions we can bound the probability of failure of a computationally unbounded adversary who places the errors. This relies  on the pseudorandom generators of Naor & Naor (but for large finite fields).

This trick applies more generally: Assume you can prove some bad event that involves a linear function of  an n length i.i.d. random vector r happens with very small probability p_{bad}.

Then instead of using the random vector, you can use a pseudo-random vector r' that is generated from only \log n random bits and still have a bound on the bad event being less than p_{bad}+ \epsilon where \epsilon is the total variation bound obtained from the pseudo-random generator.

On Secure Distributed Data Storage Under Repair Dynamics

by Sameer Pawar, Salim El Rouayheb, Kannan Ramchandran

Sameer presented his work the repair problem under secrecy constraints. The problem is to construct a distributed storage system that stays secure when repairs are taking place. The model is that an eavesdropper can observe the data arriving at \ell nodes in an (n,k) distributed storage system. The static version of this problem (no repairs) is equivalent to the erasure-erasure wiretap-II channel studied in this paper by Arunkumar and Mclaughlin while this paper generalizes this problem under the natural repair dynamics. As far as I understood, there were two results. One was a general bound on the secrecy capacity for any distributed storage system. There is also a surprising separation result:

For distributed storage operating at the minimum bandwidth point (MBR) secrecy and repair can be separated without loss of optimality. The authors show that the combination of using an MDS code to achieve secrecy (by ‘mixing’ the data with random noise keys) and exact Minimum bandwidth regenerating codes that were recently invented in this paper by Rashmi et al. for repair, achieves the secrecy capacity.

Interestingly, the same separation is no longer optimal for other points of the storage-repair tradeoff and as far as I understood the secrecy capacity remains open.

Codes for Distributed Storage: The repair problem

Posted on by

The first two talks in this session

Explicit and Optimal Exact-Regenerating Codes for the Minimum-Bandwidth Point in Distributed Storage by K. V. Rashmi , Nihar B. Shah , P. Vijay Kumar , Kannan Ramchandran

and

A Flexible Class of Regenerating Codes for Distributed Storage by Nihar B. Shah, K. V. Rashmi, P. Vijay Kumar

where given by Vijay Kumar.  To summarize the results in these two papers (and also

Exact-Repair MDS Codes for Distributed Storage Using Interference Alignment

by Changho Suh and Kannan Ramchandran

that appeared in another session), it is useful to briefly explain the current landscape of the repair problem:

(for more information see the Distributed storage wiki and this survey paper which however do not contain these new results yet.)

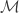Assume a file to be stored, of size B (sometimes also found as \mathcal{M} in the literature) one can use an (n,k) MDS code for storage with maximum reliability: just cut the file into k packets of size B/k, encode into n pieces (of the same size \alpha=B/k ) and store each packet into a storage node. The reliability achieved is that any k storage nodes contain enough information to recover the file, which is the best possible. 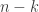So we can tolerate any n-k failures without losing data. But most of the time we only have one failure. We then want to repair this failure by creating a new encoded packet by communicating as little information as possible from d  surviving storage nodes. There are two cases:

1. If we ask that the new packet still forms a good code (i.e. any k out of the new n nodes suffice to recover), the problem is called functional repair and is completely solved and equivalent to multicasting.  The minimum repair bandwidth can be determined by a cut-set bound and we will refer to the achievable region as the cut-set region.

2. If we ask that the new packet formed is exactly identical to the lost one: This problem is called exact repair and is very difficult. It is equivalent to a multicasting network coding problem with intermediate nodes having requests for subsets and therefore prior tools from network coding do not suffice. The repair problem seems close to locally decodable codes but this connection has not been investigated yet.

The amount of information communicated from d surviving nodes is called the repair bandwidth \gamma=d\beta. Another issue is that one can reduce this repair bandwidth if the storage per node \alpha is allowed to increase and there is a tradeoff involved.

The two most important points of this tradeoff are called Minimum Storage point (MSR)  (where \alpha=B/k corresponds to MDS codes) and Minimum Bandwidth point (MBR) (where \alpha is larger but the repair bandwidth is minimized).

Clearly exact repair is a strictly harder than functional repair and the cut-set region is still a valid outer bound. A substantial amount of recent work has been focused on understanding the communication required for exact repair. All the results here establish that the cut-set region is achievable for exact repair for the parameters discussed.

Vijay presented a storyline that concluded to the settings which were known before.

This paper had completely solved the problem for the Minimum Bandwidth (MBR) point, for any (n,k), but fixing d=n-1.

The first paper (Explicit and Optimal Exact-Regenerating Codes for the Minimum-Bandwidth Point in Distributed Storage) in this session established that the MBR cut-set bound point can be achieved with exact repair for any d, corresponding to an arbitrary number d\leq n-k of failed nodes. The second result in this paper is that all the other interior points of the tradeoff curve (except the points of minimum repair and minimum storage) cannot be achieved with linear codes for exact repair. ( Of course this does not preclude the possibility that they can be approached infinitely close by making the code packets smaller and smaller).

In the second paper A Flexible Class of Regenerating Codes for Distributed Storage, the authors generalize the requirements of the distributed storage system: the initial requirement was that any data collector who connects to any k storage nodes (and receives all their stored data ) obtains enough information to recover the file. Here the authors want to enable data collectors who have limited communication with each storage node to reconstruct the file. The only requirement is that the total amount of information communicated is sufficient. This is, of course, a harder requirement on the storage code and the authors characterize the repair bandwidth for functional repair under this new requirement of flexible recovery. The technical part involves graph theoretically bounding the flow for these flexible information flow graphs. The question of exact repair of these flexible regenerating codes naturally arises and it seems to me that previous exact regenerating code constructions do not immediately generalize.

Finally, in another session was the closely related paper

Exact-Repair MDS Codes for Distributed Storage Using Interference Alignment

by Changho Suh and Kannan Ramchandran

Changho presented two new results: both are for the minimum storage point (MSR) and hence correspond to results for MDS codes.

One is that for the low-rate regime k/n \leq 1/2 if the number of nodes helping for the repair is sufficiently large d \geq 2k-1,  the MSR cut-set point can be achived for exact repair. For this regime the paper presents explicit code constructions that use a small finite fields and build on this paper which established similar results but only when repairing systematic nodes (and not nodes storing parities).

The second result of this paper closes the open problem of MSR exact repair for the high-rate 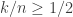k/n\geq 1/2 regime. The paper uses the symbol extension technique introduced in the Cadambe-Jafar paper Interference Alignment and the Degrees of Freedom for the K User Interference Channel to MDS codes that asymptotically approach the cut-set bound.

This paper appeared simultaneously with

Distributed Data Storage with Minimum Storage Regenerating Codes – Exact and Functional Repair are Asymptotically Equally Efficient, by Viveck R. Cadambe, Syed A. Jafar, Hamed Maleki,

Which independently obtain very similar results using the same technique. Note that the symbol extension approach requires vector linear network coding (sub-packetization of each stored packet) and to approach the cut-set bound an enormous amount of subpacketization (and field size) seem to be required. I think it is correct to interpret these results as existence proofs of high-rate regenerating codes approaching the cut-set bound for exact repair, rather than explicit constructions.

I think that the applicability of interference alignment to problems that seem to have nothing to do with wireless channels is quite remarkable. Another related case is the paper

Network Coding for Multiple Unicasts: An Interference Alignment Approach

by A. Das, S. Vishwanath, S. Jafar, A. Markopoulou.

I will blog my notes on this paper (hopefully) soon. Are the slides available anywhere? I took pictures of slides from other talks but my camera run out of battery.

ISIT 2010 : error analysis and asynchrony

Posted on by

The remaining blogging from ISIT on my end will probably be delayed a bit longer since I have camera deadlines for EVT and ITW, a paper with Can Aysal for the special SP gossip issue that is within epsilon of getting done (and hence keeps getting put off) and a paper for Allerton with Michele Wigger and Young-Han Kim that needs some TLC. Phew! Maybe Alex will pick up the slack… (hint, hint)

Asynchronous Capacity per Unit Cost (Venkat Chandar, Aslan Tchamkerten, David Tse)
This paper was the lone non-adversarial coding paper in the session my paper was in. Aslan talked about a model for coding in which you have a large time block [0,A] in which B bits arrive at a random time at the encoder. The bits have to be transmitted to the receiver with delay less than D. The decoder hears noise when the encoder is silent, and furthermore doesn’t know when the encoder starts transmitting. They both know A, however. They do a capacity per-unit-cost analysis for this system and give capacity results in various cases, such as whether or not there is is a 0-cost symbol, whether or not the delay is subexponential in the number of bits to be sent, and so on.

Moderate Deviation Analysis of Channel Coding: Discrete Memoryless Case (Yucel Altug, Aaron Wagner)
This was a paper that looked at a kind of intermediate behavior in summing and normalizing random variables. If you sum up n iid variables and normalize by n you get a law of large numbers and large deviations analysis. If you normalized by \sqrt{n} you get a central limit theorem (CLT). What if you normalize by n^{2/3} for example? It turns out you get something like
\mathbb{P}( \frac{1}{n^{\beta}} \sum_{i=1}^{n} X_i \ge \epsilon ) \le \exp( -n^{2 \beta - 1} I_{\mathcal{N}}(\epsilon) )
where I_{\mathcal{N}}(\epsilon) is the rate function for the Gaussian you get out of the CLT. This is useful for error exponent analysis because it lets you get a handle on how fast you can get the error to decay if your sequence of codes has rate tending to capacity. They use these techniques to show that for a sequence of codes with gaps \epsilon_n to capacity the error decays like \exp( - n \epsilon_n^2/(2 \sigma), where \sigma is the dispersion of the channel.

Minimum energy to send k bits with and without feedback (Yury Polyanskiy, H. Vincent Poor, Sergio Verdu)
This was on the energy to send a bit but in the non-asymptotic energy regime (keeping philosophically with the earlier line of work by the authors) for the AWGN channel. Without feedback they show an achievability and converse for sending M codewords with error \epsilon and energy E. These give matching scalings up to the first three terms as E \to \infty. The first term is (E/N_0) \log e. Interestingly, with feedback, they show that the first term is 1/(1 - \epsilon) times the term without feedback, which makes sense since as the error goes to 0 the rates should coincide. They also have a surprising result showing that with energy E > k N_0 you can send 2^k messages with 0 error.