DIMACS Workshop on Distributed Optimization, Information Processing, and Learning

Posted on March 12, 2017 by Anand Sarwate

My colleague Waheed Bajwa, Alejandro Ribeiro, and Alekh Agarwal are organizing a Workshop on Distributed Optimization, Information Processing, and Learning from August 21 to August 23, 2017 at Rutgers DIMACS. The purpose of this workshop is to bring together researchers from the fields of machine learning, signal processing, and optimization for cross-pollination of ideas related to the problems of distributed optimization, information processing, and learning. All in all, we are expecting to have 20 to 26 invited talks from leading researchers working in these areas as well as around 20 contributed posters in the workshop.

Registration is open from now until August 14 — hope to see some of you there!

2015 Bellairs Workshop on Large-Scale Inference and Optimization

Posted on March 8, 2015 by Anand Sarwate

A few weeks ago I got to go to Bellairs in Holetown, Barbados for a workshop organized by Mike Rabbat and Mark Coates of McGill University. It’s a small workshop, mostly for Mike and Mark’s students, and it’s a chance to interact closely and perhaps start some new research collaborations. Here’s a brief summary of the workshop as I remember it from my notes.

Continue reading →

Postdoctoral position at University of Michigan

Posted on October 10, 2014 by Anand Sarwate

A postdoctoral position is available at the University of Michigan Electrical Engineering and Computer Science Department for a project related to anomaly detection in networked cyber-physical systems. The successful applicant will have knowledge in one or more of the following topics: convex optimization and relaxations, compressed sensing, distributed optimization, submodularity, control and dynamical systems or system identification. The project will cover both theory and algorithm development and some practical applications in fault and attack detection in transportation and energy networks. The position can start anytime in 2014 or early 2015. This is a one year position, renewable for a second year. Interested candidates should contact Necmiye Ozay at necmiye@umich.edu with a CV and some pointers to representative publications.

ISIT 2014: how many samples do we need?

Posted on July 24, 2014 by Anand Sarwate

Due to jetlag, my CAREER proposal deadline, and perhaps a bit of general laziness, I didn’t take as many notes at ISIT as I would have, so my posting will be somewhat light (in addition to being almost a month delayed). If someone else took notes on some talks and wants to guest-post on it, let me know!

Strong Large Deviations for Composite Hypothesis Testing
Yen-Wei Huang (Microsoft Corporation, USA); Pierre Moulin (University of Illinois at Urbana-Champaign, USA)
This talk was actually given by Vincent Tan since neither of the authors could make it (this seems to be a theme of talks I’ve attended this summer. The paper was about testing a simple hypothesis 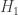$H_1$ versus a composite hypothesis 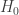$H_0$ where under 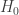$H_0$ the observations are i.i.d. with respect to one of possibly $k$ different distributions. There are therefore $k$ different errors and the goal is to characterize these errors when we ask for the probability of true detection to be greater than $1 - \epsilon$ . This is a sort of generalized Neyman-Pearson setup. They look at the vector of log-likelihood ratios and show that a threshold test is nearly optimal. At the time, I understood the idea of the proof, but I think it’s one of things where you need to really read the paper.

Randomized Sketches of Convex Programs with Sharp Guarantees
Mert Pilanci (University of California, Berkeley, USA); Martin J. Wainwright (University of California, Berkeley, USA)
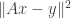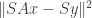This talk was about using random projections to lower the complexity of solving a convex program. Suppose we want to minimize $\| Ax - y \|^2$ over $x$ given $y$ . A sketch would be to solve $\| SAx - Sy \|^2$ where $S$ is a random projection. One question is how to choose $A$ . 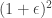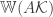They show that choosing $S$ to be a randomized Hadamard matrix (the paper studies Gaussian matrices), then the objective value of the sketched program is at most $(1 + \epsilon)^2$ times the value of the original program as long as the the number of rows of $S$ is larger than $O( \epsilon^{-2} \mathbb{W}^2(A \mathcal{K}))$ , where $\mathbb{W}(A \mathcal{K})$ is the Gaussian width of the tangent cone of the contraint set at the optimum value. For more details look at their preprint on ArXiV.

On Efficiency and Low Sample Complexity in Phase Retrieval
Youssef Mroueh (MIT-IIT, USA); Lorenzo Rosasco (DIBRIS, Unige and LCSL – MIT, IIT, USA)
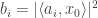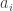This was another talk not given by the authors. The problem is recovery of a complex vector $x_0 \in \mathbb{C}^n$ from phaseless measurements of the form $b_i = |\langle a_i, x_0 \rangle|^2$ where $a_i$ are complex spherically symmetric Gaussian vectors. Recovery from such measurements is nonconvex and tricky, but an alternating minimizing algorithm can reach a local optimum, and if you start it in a “good” initial position, it will find a global optimum. The contribution of this paper is provide such a smart initialization. The idea is to “pair” the measurements to create new measurements $y_i = \mathrm{sign}( b_i^{(1)} - b_i^{(2)} )$ . This leads to a new problem (with half as many measurements) which is still hard, so they find a convex relaxation of that. I had thought briefly about such sensing setups a long time ago (and by thought, I mean puzzled over it at a coffeshop once), so it was interesting to see what was known about the problem.

Sorting with adversarial comparators and application to density estimation
Jayadev Acharya (University of California, San Diego, USA); Ashkan Jafarpour (University of California, San Diego, USA); Alon Orlitsky (University of California, San Diego, USA); Ananda Theertha Suresh (University of California, San Diego, USA)
Ashkan gave this talk on a problem where you have $m$ samples from an unknown distribution $p$ and a set of distributions $\{q_1, q_2, \ldots, q_n\}$ to compare against. You want to find the distribution that is closest in 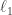$\ell_1$ . One way to do this is via Scheffe tournament tht compares all pairs of distributions — this runs in time 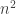$n^2$ time. They show a method that runs in 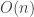$O(n)$ time by studying the structure of the comparators used in the sorting method. The motivation is that running comparisons can be expensive (especially if they involve human decisions) so we want to minimize the number of comparisons. The paper is significantly different than the talk, but I think it would definitely be interesting to those interested in discrete algorithms. The density estimation problem is really just a motivator — the sorting problem is far more general.

ICML 2014: a few more papers

Posted on July 18, 2014 by Anand Sarwate

After a long stint of proposal writing, I figured I should catch up on some old languishing posts. So here’s a few quick notes on the remainder of ICML 2014.

Fast Stochastic Alternating Direction Method of Multipliers (Wenliang Zhong; James Kwok): Most of the talks in the Optimization II session were on ADMM or stochastic optimization, or both. This was int he last category. ADMM can have rather high-complexity update rules, especially on large, complex problems, so the goal is to lower the complexity of the update step by making it stochastic. The hard part seems to be controlling the step size.
An Asynchronous Parallel Stochastic Coordinate Descent Algorithm (Ji Liu; Steve Wright; Christopher Re; Victor Bittorf; Srikrishna Sridhar): The full version of this paper is on ArXiV. The authors look at a multi-core lock-free stochastic coordinate descent method and characterize how many cores you need to get linear speedups — this depends on the convexity properties of the objective function.
Communication-Efficient Distributed Optimization using an Approximate Newton-type Method (Ohad Shamir; Nati Srebro; Tong Zhang): This paper looked 1-shot “average at the end” schemes where you divide the data onto multiple machines, have them each train a linear predictor (for example) using stochastic optimization and then average the results. This is just averaging i.i.d. copies of some complicated random variable (the output of an optimization) so you would expect some variance reduction. This method has been studied by a few people int the last few years. While you do get variance reduction, the bias can still be bad. On the other extreme, communicating at every iteration essentially transmits the entire data set (or worse) over the network. They propose a new method for limiting communication by computing an approximate Newton step without approximating the full Hessian. It works pretty well.
Lower Bounds for the Gibbs Sampler over Mixtures of Gaussians (Christopher Tosh; Sanjoy Dasgupta): This was a great talk about how MCMC can be really slow to converge. The model is a mixture of Gaussians with random weights (Dirichlet) and means (Gaussian I think). Since the posterior on the parameters is hard to compute, you might want to do Gibbs sampling. They use conductance methods to get a lower bound on the mixing time of the chain. The tricky part is that the cluster labels are permutation invariant — I don’t care if you label clusters (1,2) versus (2,1), so they need to construct some equivalence classes. They also have further results on what happens when the number of clusters is misspecified. I really liked this talk because MCMC always seems like black magic to me (and I even used it in a paper!)
(Near) Dimension Independent Risk Bounds for Differentially Private Learning (Prateek Jain; Abhradeep Guha Thakurta): Abhradeep presented a really nice paper with a tighter analysis of output and objective perturbation methods for differentially private ERM, along with a new algorithm for risk minimization on the simplex. Abhradeep really only talked about the first part. If you focus on scalar regret, they show that essentially the error comes from taking the inner product of a noise vector with a data vector. If the noise is Gaussian then the noise level is dimension-independent for bounded data. This shows that taking $(\epsilon,\delta)$ -differential privacy yield better sample complexity results than $(\epsilon,)$ -differential privacy. This feels similar in flavor to a recent preprint on ArXiV by Beimel, Nissim, and Stemmer.
Near-Optimally Teaching the Crowd to Classify (Adish Singla; Ilija Bogunovic; Gabor Bartok; Amin Karbasi; Andreas Krause): This was one of those talks where I would have to go back to look at the paper a bit more. The idea is that you want to train annotators to do better in a crowd system like Mechanical Turk — which examples should you give them to improve their performance? They model the learners as doing some multiplicative weights update. Under that model, the teacher has to optimize to pick a batch of examples to give to the learner. This is hard, so they use a submodular surrogate function and optimize over that.
Discrete Chebyshev Classifiers (Elad Eban; Elad Mezuman; Amir Globerson): This was an award-winner. The setup is that you have categorical (not numerical) features on $n$ variables and you want to do some classification. They consider taking pairwise inputs and compute for each tuple $(x_i, x_j, y)$ a marginal $\mu_{ij}(x_i, x_j, y)$ . If you want to create a rule $f: \mathcal{X} \to \mathcal{Y}$ for classification, you might want to pick one that has best worst-case performance. One approach is to take the one which has best worst-case performance over all joint distributions on all variables that agree with the empirical marginals. This optimization looks hard because of the exponential number of variables, but they in fact show via convex duality and LP relaxations that it can be solved efficiently. To which I say: wow! More details are in the paper, but the proofs seem to be waiting for a journal version.

yet more not-so-recent hits from ArXiV

Posted on May 8, 2014 by Anand Sarwate

Some shorter takes on these papers, some of which I should read in more detail later. I figure I’ll use the blog for some quick notes and to see if any readers have any comments/ideas about these:

Differentially Private Convex Optimization with Piecewise Affine Objectives (Shuo Han, Ufuk Topcu, George J. Pappas) — arXiv:1403.6135 [math.OC]. The idea here is to look at minimizing functions of the form
$f(x) = \max_{i = 1,2, \ldots, m} \{ a_i^{\top} x + b_i \}$
subject to $x$ belonging to some convex polytope $\mathcal{P}$ . This is a bit different than the kind of convex programs I’ve been looking at (which are more ERM-like). Such programs occur often in resource allocation problems. Here the private information of users are the offsets $b_i$ . They propose a number of methods for generating differentially private approximations to this problem. Analyzing the sensitivity of this optimization is tricky, so they use an upper bound based on the diameter of the feasible set $\mathcal{P}$ to find an appropriate noise variance. The exponential mechanism also gives a feasible mechanism, although the exact dependence of the suboptimality gap on $\epsilon$ is unclear. They also propose a noisy subgradient method where, instead of using SGD, they alter the sampling distribution using the exponential mechanism to choose a gradient step. Some preliminary experiments are also given (although none exploring the dependence on $\epsilon$ , which would also be very interesting)!

Assisted Common Information with an Application to Secure Two-Party Sampling (Vinod M. Prabhakaran, Manoj M. Prabhakaran) — arXiv:1206.1282 [cs.IT]. This is the final version of the journal version of a few conference papers that Vinod and Manoj have done on an interesting variant of the Gács-Körner problem. The motivation is from secure multiparty computation — the problem also touches on some work Vinod and I started but is sadly languishing due to the utter overwhelmingness of starting a new job. Hopefully I can get back to it this summer.

Analysis of Distributed Stochastic Dual Coordinate Ascent (Tianbao Yang, Shenghuo Zhu, Rong Jin, Yuanqing Lin) — arXiv:1312.1031 [cs.DC]. The title pretty much sums it up. I’m interested in looking a bit more at the analysis method, since I had a similar algorithm bouncing around my head that I would like to analyze. The main idea is also update the primal variables to achieve a speedup/use a larger step size.

Convergence of Stochastic Proximal Gradient Algorithm (Lorenzo Rosasco, Silvia Villa, Bang Công Vũ) — arXiv:1403.5074 [math.OC]. This is a similar setup as my last post, with a convex objective that has a smooth and non-smooth component. They show convergence in expectation and almost surely. The key here is that they show convergence in an infinite-dimentionsal Hilbert space instead of, say, $\mathbb{R}^d$ .

more not-so-recent hits from ArXiV

Posted on April 24, 2014 by Anand Sarwate

arXiv:1403.4696 [math.OC]
Design and Analysis of Distributed Averaging with Quantized Communication
Mahmoud El Chamie, Ji Liu, Tamer Başar

The goal of this paper is to analyze the “performance of a subclass of deterministic distributed averaging algorithms where the information exchange between neighboring nodes (agents) is subject to uniform quantization.” I was interested in the connections to Lavaei and Murray’s TAC paper. Here though, they consider a standard consensus setup with a doubly stochastic weight matrix $W$ and deterministic, rather than randomized, quantization. They consider two types — rounding and truncation (essentially the floor operation). The update rule is $x_i(t+1) = x_i(t) + \sum_{j} W_{ij} (Q(x_j(t)) - Q(x_i(t)))$ where $Q$ is the quantization operation. They shoe that in finite time the agents either reach a consensus on the floor of the average of their initial values, or that the cycle indefinitely in a neighborhood around the average. They they show how to control the size of the neighborhood in a decentralized way. There are a lot of works on quantized consensus that have appeared in the last 5 years, and to be honest I haven’t really kept up on the recent literature, so I’m not sure how to compare this to the other works that have appeared, but perhaps some of the readers of the blog have…

arXiv:1403.4699 [math.OC]
A Proximal Stochastic Gradient Method with Progressive Variance Reduction
Lin Xiao, Tong Zhang

This paper looks at convex optimization problems of the form

$\min_{x \in \mathbb{R}^d} F(x) + R(x)$

where the overall objective $P(x) + R(x)$ is strongly convex, the regularizer $R(x)$ is lower semicontinuous and convex, and the term $F(x) = \frac{1}{n} \sum_{i=1}^{n} f_i(x)$ separates into a sum of function $f_i(x)$ which are Lipschitz continuous. The proximal gradient method is an iterative procedure for solving this program that does the following:

$x_{t} = \mathrm{argmin}_{x \in \mathbb{R}^d} \left\{ \nabla F(x_{t})^{\top} x + \frac{1}{2 \eta_t} \| x - x_{t-1} \|^2 + R(x) \right\}$

If we define the $\mathrm{prox}_{R}$ function as

$\mathrm{prox}_R(y) = \mathrm{argmin}_{x \in \mathbb{R}^d} \left\{ \frac{1}{2} \|x - y\|^2 + R(x) \right\}$

then the step looks like:

$x_t = \mathrm{prox}_{\eta_t R}(x_{t-1} - \eta_{t} \nabla F(x_{t-1}))$

A stochastic gradient (SG) version of this is

$x_t = \mathrm{prox}_{\eta_t R}(x_{t-1} - \eta_{t} \nabla f_{i_t}(x_{t-1}))$

where $i_t$ is sampled uniformly from $\{1,2,\ldots, n\}$ at each time. The advantage of the SG variant is that it takes less time to do one iteration, but each iteration is much noisier. The goal of this paper is to adapt a previous method/approach to variance reduction to improve the performance of the Prox-SG algorithm. The approach is one or resampling points according to the Lipschitz constants. This sort of “sampling based adaptivity” was also used by my ex-colleague Samory Kpotufe and collaborators in their NIPS paper from 2012 (a longer version is under review). At least I think they’re related.

arXiv:1403.5341v1 [cs.LG]
An Information-Theoretic Analysis of Thompson Sampling
Daniel Russo, Benjamin Van Roy

In a multi-armed bandit problem we have a set of actions (arms) $A$ and at each time the learner picks an action $a$ and observes an outcome $Y_t(a) \in \mathcal{Y}$ which is assigned a reward by a function $R: \mathcal{Y} \to \mathbb{R}$ . The rewards are assumed to be i.i.d. across time for each action with distributions $p(y | a)$ that are unknown to the learner. The goal is to maximize the reward, which is the same as finding the arm with the largest expected reward. This leads to a classical explore/exploit tradeoff where the learner has to decide whether to explore new arms which may have higher expected reward, or continue exploiting the reward offered by the current arm. Thompson sampling is a Bayesian approach where the learner starts with a prior on the best action and then samples actions at each time according to its posterior belief on the best arm. The authors here analyze the regret of such a policy in terms of what they call the information gain of the system. This gain depends on the ratio between two quantities that are functions of the outcome distributions $p(y | a)$ . One is what they call the “divergence in mean,” namely the difference in expected reward between arms, and the other is the KL divergence.

Some (not-so-)recent hits from ArXiV

Posted on April 15, 2014 by Anand Sarwate

I always end up bookmarking a bunch of papers from ArXiV and then looking at them a bit later than I want. So here are a few notes on some papers from the last month. I have a backlog of reading to catch up on, so I’ll probably split this into a couple of posts.

arXiv:1403.3465v1 [cs.LG]: Analysis Techniques for Adaptive Online Learning
H. Brendan McMahan
This is a nice survey on online learning/optimization algorithms that adapt to the data. These are all variants of the Follow-The-Regularized-Leader algorithms. The goal is to provide a more unified analysis of online algorithms where the regularization is data dependent. The intuition (as I see it) is that you’re doing a kind of online covariance estimation and then regularizing with respect to the distribution as you are learning it. Examples include the McMahan and Streeter (2010) paper and the Duchi et al. (2011) paper. Such adaptive regularizers also appear in dual averaging methods, where they are called “prox-functions.” This is a useful survey, especially if, like me, you’ve kind of checked in and out with the online learning literature and so may be missing the forest for the trees. Or is that the FoReL for the trees?

arXiv:1403.4011 [cs.IT]: Whose Opinion to follow in Multihypothesis Social Learning? A Large Deviation Perspective
Wee Peng Tay
This is a sort of learning from expert advice problem, though not in the setting that machine learners would consider it. The more control-oriented folks would recognize it as a multiple-hypothesis test. The model is that there is a single agent (agent $0$ ) and $K$ experts (agents $1, 2, \ldots, K$ ). The agent is trying to do an $M$ -ary hypothesis test. The experts (and the agent) have access to local (private) observations $Y_k[1], Y_k[2], \ldots, Y_k[n_k]$ for $k \in \{0,1,2,\ldots,K\}$ . The observations come from a family of distributions determined by the true hypothesis $m$ . The agent $0$ needs to pick one of the $K$ experts to hire — the analogy is that you are an investor picking an analyst to hire. Each expert has its own local loss function $C_k$ which is a function of the amount of data it has as well as the true hypothesis and the decision it makes. This is supposed to model a “bias” for the expert — for example, they may not care to distinguish between two hypotheses. The rest of the paper looks at finding policies/decision rules for the agents that optimize the exponents with respect to their local loss functions, and then looking at how agent $0$ should act to incorporate that advice. This paper is a little out of my wheelhouse, but it seemed interesting enough to take a look at. In particular, it might be interesting to some readers out there.

arXiv:1403.3862 [math.OC] Asynchronous Stochastic Coordinate Descent: Parallelism and Convergence Properties
Ji Liu, Stephen J. Wright
This is another paper on lock-free optimization (c.f. HOGWILD!). The key difference, as stated in the introduction, is that they “do not assume that the evaluation vector $\hat{x}$ is a version of $x$ that actually existed in the shared memory at some point in time.” What does this mean? It means that a local processor, when it reads the current state of the iterate, may be performing an update with respect to a point not on the sample path of the algorithm. They do assume that the delay between reading and updating the common state is bounded. To analyze this method they need to use a different analysis technique. The analysis is a bit involved and I’ll have to take a deeper look to understand it better, but from a birds-eye view this would make sense as long as the step size is chosen properly and the “hybrid” updates can be shown to be not too far from the original sample path. That’s the stochastic approximator in me talking though.

More ArXiV skims

Posted on April 23, 2013 by Anand Sarwate

Assumptionless consistency of the Lasso
Sourav Chatterjee
The title says it all. Given $p$ -dimensional data points $\{ \mathbf{x}_i : i \in [n] \}$ the Lasso tries to fit the model $\mathbb{E}( y_i | \mathbf{x_i}) = \boldsymbol{\beta} \mathbf{x}_i$ by minimizing the $\ell^1$ penalized squared error
$\sum_{i=1}^{n} (y_i - \boldsymbol{\beta} \mathbf{x}_i)^2 + \lambda \| \boldsymbol{\beta} \|_1$ .
The paper analyzes the Lasso in the setting where the data are random, so there are $n$ i.i.d. copies of a pair of random variables $(\mathbf{X},Y)$ so the data is $\{(\mathbf{X}_i, Y_i) : i \in [n] \}$ . The assumptions are on the random variables $(\mathbf{X},Y)$ : (1) each coordinate $|X_i| \le M$ is bounded, the variable $Y = (\boldsymbol{\beta}^*)^T \mathbf{X} + \varepsilon$ , and $\varepsilon \sim \mathcal{N}(0,\sigma^2)$ , where $\boldsymbol{\beta}^*$ and $\sigma$ are unknown constants. Basically that’s all that’s needed — given a bound on $\|\boldsymbol{\beta}\|_1$ , he derives a bound on the mean-squared prediction error.

On Learnability, Complexity and Stability
Silvia Villa, Lorenzo Rosasco, Tomaso Poggio
This is a handy survey on the three topics in the title. It’s only 10 pages long, so it’s a nice fast read.

Adaptivity of averaged stochastic gradient descent to local strong convexity for logistic regression
Francis Bach
A central challenge in stochastic optimization is understanding when the convergence rate of the excess loss, which is usually $O(1/\sqrt{n})$ , can be improved to $O(1/n)$ . Most often this involves additional assumptions on the loss functions (which can sometimes get a bit baroque and hard to check). This paper considers constant step-size algorithms but where instead they consider the averaged iterate $\latex \bar{\theta}_n = \sum_{k=0}^{n-1} \theta_k$. I’m trying to slot this in with other things I know about stochastic optimization still, but it’s definitely worth a skim if you’re interested in the topic.

On Differentially Private Filtering for Event Streams
Jerome Le Ny
Jerome Le Ny has been putting differential privacy into signal processing and control contexts for the past year, and this is another paper in that line of work. This is important because we’re still trying to understand how time-series data can be handled in the differential privacy setting. This paper looks at “event streams” which are discrete-valued continuous-time signals (think of count processes), and the problem is to design a differentially private filtering system for such signals.

Gossips and Prejudices: Ergodic Randomized Dynamics in Social Networks
Paolo Frasca, Chiara Ravazzi, Roberto Tempo, Hideaki Ishii
This appears to be a gossip version of Acemoglu et al.’s work on “stubborn” agents in the consensus setting. They show similar qualitative behavior — opinions fluctuate but their average over time converges (the process is ergodic). This version of the paper has more of a tutorial feel to it, so the results are a bit easier to parse.

Bellairs Workshop 2013

Posted on February 23, 2013 by Anand Sarwate

I just wanted to write a few words about the workshop at the Bellairs Research Institute. I just returned from sunny Barbados to frigid Chicago, so writing this will help me remember the sunshine and sand:

The beach at Bathsheba on the east coast of Barbados

Mike Rabbat put on a great program this year, and there were lots of talks on a range of topics in machine learning, signal processing, and optimization. The format of the workshop was to have talks with lots of room for questions and discussion. Talks were given out on the balcony where we were staying, and we had to end at about 2:30 because the sunshine would creep into our conference area, baking those of us sitting too far west.