Monthly Archives: February 2010

Noose at UCSD Library

Posted on by

A noose was found at the UCSD library, and the campus police have issued a report calling it “[h]anging a noose with intent to terrorize.” It’s unclear if the incident is related to the recent outcry over the off-campus “Compton Cookout” party. During a recent teach-in, there was a massive walk-out by students angry at the school’s response. There are going to be new protests today over the noose incident.

update: I say that it’s unclear if it is connected but what I really mean is that it’s not clear if the party organizers are involved. The timing is too close for it to be unrelated. I would not be surprised if it turns out to be some idiot’s bad idea of a “joke” or “site-specific provocative art.”

update 2: A student has contacted the police and confessed to placing the noose. No other news, however.

update 3: Students are occupying the chancellor’s office.

update 4: More updates here.

Pitfalls in author ordering

Posted on by

Apparently the number of co-authored papers in political science is on the rise, and there are questions on how to order the author names. I had never heard the phrase “the tyranny of the alphabet” before to refer to alphabetical author ordering, but I know that since conventions are different in math/statistics, computer science, and electrical engineering, there ends up being a lot of confusion (esp. on the part of graduate students) as to who actually did “most of the work” on a paper. Fan Chung Graham gives a succinct description of an ideal:

In math, we use the Hardy-Littlewood rule. That is, authors are alphabetically ordered and everyone gets an equal share of credit. The one who has worked the most has learned the most and is therefore in the best position to write more papers on the topic.

This ideal doesn’t really hold in electrical engineering (or computer science, for that matter), and can lead to some dangerous assumptions when people’s conventions vary or when you are doing interdisciplinary work.

Continue reading →

Privacy Workshop at IPAM

Posted on by

I’m at the Institute for Pure and Applied Math at a workshop on Statistical and Learning-Theoretic Challenges in Data Privacy. It’s a rather diverse group of computer scientists, statisticians, medical informatics, and policy researchers, and I feel a bit like I’m the only electrical engineer here. It’sa been pretty educational in the “learning about new problems” way, but I think by the time Friday morning rolls around I’ll be suffering from information overload. The nice thing is that the slides are posted online so I can refresh my memory when I get back. There’s also a poster session for some more recent results.

Most of the speakers have been talking about either (a) applications of the differential privacy model to some problems (e.g. data release, function computation, classification, PAC-learning, auctions, or Google’s MapReduce, the Census Bureau’s OnTheMap, and PINQ)or (b) areas in which privacy is a real problem (hospital discharge data and the dangers of re-identification, genome-wide association studies (GWAS), query logs from search engines, or (c) bridges between fields and their privacy definitions and models.

I’ve just started working in this area, so I’m still processing things (the talks range from high level to technical, and I often lack the background to understand fully what’s going on). I might blog a bit more about it as things come up.

notes on a review

Posted on by

I received the following TPC review recently (a rejection):

The current version of the paper is incomplete, as important proofs (the novel results…) are left to supplementary material. This can be resolved, however would require a major structural change.

I think I would have preferred the TPC to simply say “we had too many papers, and yours wasn’t in the top X%,” rather then append this completely nonsensical reason for rejection. We put the proofs in the supplementary material because of space constraints. We could just as easily have omitted other things and put the proofs in the main body by doing some minor cutting and pasting. It may be a “major structural change,” but its also trivial. Perhaps they thought the paper was poorly written, but they did not say that.

Of course I’m disappointed that the paper wasn’t accepted, especially given that all the reviewers recommended acceptance. It’s clear that the real reason the TPC rejected us was that the scores were not high enough and they had to reject a lot of papers. It sucks to be on the bad side of a subjective decision, but it happens to everyone. Making up a pseudo-objective reason is about as useful as a little white lie. As it is, this description is about as principled as “your paper has too many authors,” or “your bibliography is too long” or “we cannot accept any more papers starting with the letter D.” There’s always the next deadline, anyway.

Bach Collegium on KPBS

Posted on by

I sang this morning with other members of the Bach Collegium San Diego on the KBPS radio show These Days. Our director, Ruben, and two singers, Anne-Marie and Martha, talked about how we’re going for Baroque this weekend in singing all six of Bach’s motets.

Also featured: comparisons between zoning out while singing Bach and wandering into a dark alley in Leipzig (followed by the Brandenburg Boys? You don’t want to mess with them!)

Concert Bleg : Bach Collegium San Diego presents all 6 Bach Motets

Posted on by

Six Bach Motets BWV 225-230 & Gala Reception

Ruben Valenzuela, Music Director

Vocalists of the Bach Collegium San Diego
Daniel Zuluaga, Lute
Shanon Zusman, Violone
Michael Sponseller, organ

Saturday, 20 February
St James by-the-Sea Episcopal Church
743 Prospect Street, La Jolla CA 92037
(Gala Reception to immediately follow in Van Schaick Room)

Sunday, 21 February
Loyola Marymount University (Murphy Recital Hall)
1 LMU Drive, Los Angeles CA 90045

Concerts at 7pm

$35 Reserved Patron
$25 General Admission
$15 Student/Senior

For tickets or other inquiries: online or (619) 341.1726

Since its founding in 2003, the Six Bach Motets have been at the core of the BCSD’s repertoire, but never ALL SIX! The motets will be performed with vocal ensembles ranging from 4-16 voices.

The San Diego concert will be immediately followed by our annual Gala Benefit Reception in the Van Schaick Room of St. James by-the-Sea. Plan now to attend both!

For combination ticket packages are available for both concert and gala. Please refer to our website for details.

McGill’s policy on “harmful consequences”

Posted on by

McGill University is contemplating ending “a requirement that any professor receiving research support from the military indicate whether the research could have ‘direct harmful consequences.'” The proponents of striking the measure say that all research should be scrutinized for harmful consequences, whereas the opponents say that it opens the gates for the US defense industry to shift the Canadian (Canadien?) research agenda.

I’m surprised they even had such a provision in the first place, given the existing injunctions against secret/classified research.

This reminds me a discussion last night at dinner, where my friend told us about a book by UCSD professor Chandra Mukerji called A Fragile Power: Scientists and the State, which talks a bit about science is dependent on state (and military funding) and how the state views scientists as a kind of “reserve force” of experts whose knowledge may become crucial later.

From Polya urns to the OK Corral

Posted on by

A new postdoc here, Punyaslok Purkayastha, pointed out to me a Probability Surveys paper by Robin Pemantle on random processes with reinforcement, and I’ve been reading through it in spare moments (usually on the bus). I have had a problem knocking about my head that is related (Ram Rajagopal and I thought we could do in our spare time but we never managed to find enough time to work on it). All this stuff is pretty well-known already, but I thought it was a nice story.

A Polya urn process starts by taking an urn with R_0 = a red balls and B_0 = b black balls at time 0. For each time 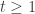t \ge 1, draw a ball uniformly from the balls in the urn and then replace it together with another ball of the same color. Let 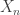X_n be the sequence of colors that you draw, where red is 0 and black is 1. So with probability R_n / (R_n + B_n) we have X_n = 0. 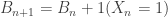The urn is updated according to R_{n+1} = R_n + 1(X_n = 0) and B_{n+1} = B_n + 1(X_n = 1).`

To figure out the asymptotic behavior of this process, just note that the sequence of colors is exchangeable. If x_1^n has k 1’s in it, then

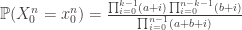
\mathbb{P}(X_0^{n} = x_0^n) = \frac{ \prod_{i = 0}^{k-1} (a + i) \prod_{i=0}^{n-k-1} (b + i)}{ \prod_{i=0}^{n-1} (a + b + i) }

From this it is clear that the probability of seeing $x_1^n$ only depends on its type (empirical distribution, for non-information theorists). Since the sequence is exchangeable, de Finetti’s Theorem shows that the fraction of red balls W_n = R_n/(R_n + B_n) converges almost surely to a random variable W, and the limit of the formula above shows that the limit is a beta distribution with parameters (a,b):

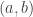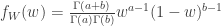
f_W(w) = \frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)} w^{a-1} (1 - w)^{b-1}

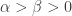A more general process is the Friedman urn process, in which you add \alpha balls of the same color you drew and \beta balls of the opposite color. If \alpha > \beta > 0 then Freedman (different spelling, different guy) showed that the proportion of red balls tends almost surely to 1/2. This happens because the evolution ends up looking like a symmetric two-state Markov chain, which has (1/2, 1/2) as its stationary distribution. Note here that the limiting fraction is almost surely constant, as opposed to there being a limiting distribution, as in the Polya process.

Let’s look at a special case where instead of adding a ball of the same color that you drew, you only add a ball of the opposite color (which is a Friedman process with parameters (0,1)). Freedman’s result doesn’t apply here, but Kingman has a nice paper (which I am reading now) relating this process to a third process: the OK Corral process.

In the OK Corral process, say we start with 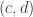(c,d) good and bad cowboys. We choose one cowboy uniformly at random and then he kills a cowboy on the opposite side. This process continues until one side has all been shot. This process is precisely the time reversal of the special Friedman urn process above. If we let 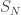S_N denote the number of surviving cowboys after the process terminates when we start with (N,N), Kingman proves that

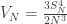
V_N = \frac{3S_N^4}{2N^3}

converges to a gamma distribution with parameter 1/2:

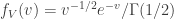
f_V(v) = v^{-1/2} e^{-v}/\Gamma(1/2)

The weird thing about this is that the scaling is 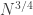N^{3/4} to get an asymptotic distribution.

Kingman and Volkov extend the analysis by embedding the urns into birth processes, which is another technique for balls-into-bins with feedback of urns with reinforcement. But that’s another story for another time (but maybe not another blog post, this one took a bit longer than I expected).