I was at the Allerton conference last week for a quick visit home — I presented a paper I wrote with Can Aysal and Alex Dimakis on analyzing broadcast-based consensus algorithms when channels vary over time. The basic intuition is that if you can get some long-range connections “enough of the time,” then you’ll get a noticeable speed up in reaching a consensus value, but with high connectivity the variance of the consensus value from the true average increases. It was a fun chance to try out some new figures that I made in OmniGraffle.

The plenary was given by Abbas El Gamal on a set of new lecture notes on network information theory that he has been developing with Young-Han Kim. He went through the organization of the material and tried to show how much of the treatment could be developed using robust typicality (see Orlitsky-Roche) and a few basic packing and covering lemmas. This in turn simplifies many of the proofs structurally and can give a unified view. Since I’ve gotten an inside peek at the notes, I can say they’re pretty good and clear, but definitely dense going at times. They are one way to answer the question of “well, what do we teach after Cover and Thomas.” They’re self-contained and compact .

What struck me is that these are really notes on network information theory and not on advanced information theory, which is the special topics class I took at Berkeley. It might be nice to have some of the “advanced but non-network” material in a little set of notes. Maybe the format of Körner’s Fourier Analysis book would work : it could cover things like strong converses, delay issues, universality, wringing lemmas, AVCs, and so on. Almost like a wiki of little technical details and so on that could serve as a reference, rather than a class. The market’s pretty small though…

I felt a bit zombified during much of the conference, so I didn’t take particularly detailed notes, but here were a few talks that I found interesting.

• Implementing Utility-Optimal CSMA (Lee, Jinsung (KAIST), Lee, Junhee (KAIST), Yi, Yung (KAIST), Chong, Song (KAIST), Proutiere, Alexandre (Microsoft Research), Chiang, Mung (Princeton University)) — There are lots of different models and algorithms for distributed scheduling in interference-limited networks. Many of these protocols involve message passing and the overhead from the messages may become heavy. This paper looked at how to use the implicit feedback from CSMA. They analyze a simple two-link system with two parameters (access and hold) and then use what I though was a “effective queue size” scheduling method. Some of the analysis was pretty tricky, using stochastic approximation tools. There were also extensive simulation results from a real deployment.
• LP Decoding Meets LP Decoding: A Connection between Channel Coding and Compressed Sensing (Dimakis, Alexandros G. (USC), Vontobel, Pascal O. (Hewlett-Packard Laboratories)) — This paper proved some connections between Linear Programming (LP) decoding of LDPC codes and goodness of compressed sensing matrices. A simple example : if a parity check matrix is good for LP decoding then it is also good for compressed sensing. In particular, if it can correct k errors it can detect k-sparse signals, and if it can correct a specific error pattern 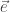it can detect all signals whose support is the same as 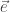. There were many other extensions of this results as well, to other performance metrics, and also the Gaussian setting.
• The Compound Capacity of Polar Codes (Hassani, Hamed (EPFL), Korada, Satish Babu (EPFL), Urbanke, Ruediger (EPFL)) — Rudi gave an overview of polar codes from two different perspectives and then showed that in general polar codes do not achieve the compound channel capacity, but it’s not clear if the problem is with the code or with the decoding algorithm (so that’s still an open question).
• Source and Channel Simulation Using Arbitrary Randomness (Altug, Yucel (Cornell University), Wagner, Aaron (Cornell University)) — The basic source simulation problem is to simulate an arbitrary source with an iid process (say equiprobable coin flips) . Using the information spectrum method, non-matching necessary and sufficient conditions can be found for when this can be done. These are in terms of sup-entropy rates and so on. Essentially though, it’s a theory built on the limits or support of the spectra of the two processes and . If the entropy spectrum in dominates that of then you’re in gravy. This paper proposed a more refined notion of dominance which looks a bit like majorization of some sort. I think they showed that was sufficient, but maybe it’s also necessary too. Things got a bit rushed towards the end.
• Channels That Die (Varshney, Lav R. (MIT), Mitter, Sanjoy K. (MIT), Goyal, Vivek K (MIT)) — This paper looked at a channel which has two states, alive (a) and dead (d), and at some random time during transmission, the channel will switch from alive to dead. For example, it might switch according to a Markov chain. Once dead, it stays dead. If you want to transmit over this channel in a Shannon-reliable sense you’re out of luck, but what you can do is try to maximize the expected number of bits you get through before the channel dies. I think they call this the “volume.” So you try to send a few bits at a time (say are the number of bits in each chunk). How do you size the chunks to maximize the volume? This can be solved with dynamic programming. There are still several open questions left, but the whole construction relies on using “optimal codes of finite blocklength” which also needs to be solved. Lav has some interesting ideas along these lines that he told me about when I was in Boston two weeks ago…
• The Feedback Capacity Region of El Gamal-Costa Deterministic Interference Channel (Suh, Changho (UC Berkeley), Tse, David (UC Berkeley)) — This paper found a single letter expression for the capacity region, which looks like the Han-Kobayashi achievable region minus the two weird constraints. Achievability uses Han-Kobayashi in a block-Markov encoding with backward decoding, and the converse uses the El Gamal-Costa argument with some additional Markov properties. For the “bit-level” deterministic channel model, there is an interpretation of the feedback as filling a “hole” in the interference graph.
• Upper Bounds to Error Probability with Feedback (Nakiboglu, Baris (MIT), Zheng, Lizhong (MIT)) — This is a follow-on to their ISIT paper, which uses a kind of “tilted posterior matching” (a phrase which means a lot to people who really know feedback and error exponents in and out) in the feedback scheme. Essentially there’s a tradeoff between getting close to decoding quickly and minimizing the error probability, and so if you change the tilting parameter in Baris’ scheme you can do a little better. He analyzes a two phase scheme (more phases would seem to be onerous).
• Infinite-Message Distributed Source Coding for Two-Terminal Interactive Computing (Ma, Nan (Boston University), Ishwar, Prakash (Boston University)) — This looked at the interactive function computation problem, in which Alice has 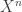, Bob has and they want to compute some functions and . The pairs 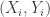are iid and jointly distributed according to some distribution . As an example, 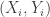could be correlated bits 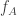and and 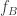could be the AND function. In previous work the authors characterized the the rate region (allowing vanishing probability of error) for rounds of communication, and here they look at the case when there are infinitely many back-and-forth messages. The key insight is to characterize the sum-rate needed as a function of — that is, to look at the function 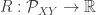and look at that surface’s analytic properties. In particular, they show it’s the minimum element of a class 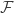of functions which have some convexity properties. There is a preprint on ArXiV.