Tag Archives: statistics

DIMACS Workshop on Distributed Optimization, Information Processing, and Learning

Posted on by

My colleague Waheed Bajwa, Alejandro Ribeiro, and Alekh Agarwal are organizing a Workshop on Distributed Optimization, Information Processing, and Learning from August 21 to August 23, 2017 at Rutgers DIMACS. The purpose of this workshop is to bring together researchers from the fields of machine learning, signal processing, and optimization for cross-pollination of ideas related to the problems of distributed optimization, information processing, and learning. All in all, we are expecting to have 20 to 26 invited talks from leading researchers working in these areas as well as around 20 contributed posters in the workshop.

Registration is open from now until August 14 — hope to see some of you there!

Signal boost: DPCOMP.ORG is live

Posted on by

I got the following email from Gerome Miklau:

Dear colleagues:

We are writing to inform you of the launch of DPCOMP.ORG.

DPCOMP.ORG is a public website designed with the following goals in mind: (1) to increase the visibility and transparency of state-of-the-art differentially private algorithms and (2) to present a principled and comprehensive empirical evaluation of these algorithms. The intended audience is both researchers who study privacy algorithms and practitioners who might deploy these algorithms.

Currently DPComp includes algorithms for answering 1- and 2-dimensional range queries. We thoroughly study algorithm accuracy and the factors that influence it and present our findings using interactive visualizations. We follow the evaluation methodology from the paper “Principled Evaluation of Differentially Private Algorithms using DPBench”. In the future we plan to extend it to cover other analysis tasks (e.g., higher dimensional data, private regression).

Our hope is that the research community will contribute to improving DPCOMP.ORG so that practitioners are exposed to emerging research developments. For example: if you have datasets which you believe would distinguish the performance of tested algorithms, new algorithms that could be included, alternative workloads, or even a new error metric, please let us know — we would like to include them.

Please share this email with interested colleagues and students. And we welcome any feedback on the website or findings.

Sincerely,

Michael Hay (Colgate University)
Ashwin Machanavajjhala (Duke University)
Gerome Miklau (UMass Amherst)

IHP “Nexus” Workshop on Privacy and Security: Day 3

Posted on by

I’m doggedly completing these notes because in a fit of ambition I actually started posts for each of the workshop days and now I feel like I need to finish it up. Day 3 was a day of differential privacy: Adam Smith, Cynthia Dwork, and Kamalika Chaudhuri.

Adam gave a tutorial on differential privacy that had a bit of a different flavor from tutorials I have seen before (and given). He started out by highlighting a taxonomy of potential attacks on released data to make a distinction between re-identification, reconstruction, membership, and correlation inferences before going into the definitions, composition theory, Bayesian interpretation, and so on. With the attacks, he focused a bit more on the reconstruction story. The algorithms view of things (as I get it) is to think of, say, an LP relaxation of a combinatorial problem: you solve the LP and round the solution to integers and prove that it’s either correct or close to correct. This has more connections to things we think about in information theory (e.g. compressed sensing) but the way of stating the problem was a bit different. He also described the Homer et al. attack on GWAS. The last part of his talk was on multiplicative weights and algorithms for learning distributions over the data domain, which I think got a bit hairy for the IT folks who hadn’t seen MW before. This made me wonder if these connections between mirror descent on the simplex, information projections, and other topics can be taught in a “first principles” way that doesn’t require you to have a lot of familiarity with one interpretation of the method before bridging to another.

Cynthia gave a talk on false discovery control and how to use differential privacy ideas in a version of the Benjamini-Hochberg BHq procedure for controlling the false discovery rate. A key primitive is the the report noisy argmax procedure, which gives the index of the argmax but not its value (which would entail a further privacy loss). Since most people are not familiar with FDR control, she spent a lot of her talk on that and so the full details of the private version were deferred to the paper. I covered FDR in my detection and estimation class partly from some of the extra attention it has received in the privacy workshops over the last few years.

Kamalika’s talk was on a model for privacy when data may be correlated between individuals. This involves using the Pufferfish model for privacy in which there is an explicit class of probability distribution on parameters and a set of explicit secrets which the algorithm wants to obfuscate: the differential privacy guarantee should hold for the output distribution of the mechanism conditioned on any valid data distribution and any pair of secrets. Since the class of data distributions is arbitrary, we can also consider joint distributions on individuals’ data — if the distribution class has some structure, then there might be a hope to efficiently produce an output of a function. She talked about using the \ell_{\infty} Wasserstein distance to measure the sensitivity of a function, and that adding noise that scales with this sensitivity would guarantee privacy in the Pufferfish model. She then gave an example for Bayesian networks and Markov chains. As we discussed, it seems like for each dependence structure you need to come up with a sort of covering of the dependencies to add noise appropriately. This seems pretty challenging in general now, but maybe after a bit more work there will be a clearer “general” strategy to handle dependence along these lines.

Signal boost: IBM Social Good Fellowship for data science

Posted on by

This announcement came via Kush Varshney. IBM is launching a new fellowship program. This came out of his work on DataKind and Saška Mojsilović’s work on Ebola. It’s open to students and postdocs!

I am pleased to let you know that Saška Mojsilović and I are launching a new fellowship program at IBM Research related to data science for social good. We are offering both 3-month summer fellowships for PhD students and full-year fellowships for postdocs. The fellowship webpage and link to apply may be found here.

Fellows will come work with research staff members at our Yorktown Heights laboratory to complete projects in partnership with NGOs, social enterprises, government agencies, or other mission-driven organizations that have large social impact. We are currently in the process of scoping projects across various areas, such as health, sustainability, poverty, hunger, equality, and disaster management. The program is intended to allow students to develop their technical skills and produce publishable work while making a positive impact on the world.

I request that you spread the word to students in your respective departments and the broader community.

Postdoctoral opportunity at NYU CS/Global Health

Posted on by

Post-doctoral opportunity in developing novel computational approaches for disease surveillance. The laboratory of Dr. Rumi Chunara in Computer Science & Engineering, and the College of Global of Public Health at New York University is seeking highly motivated researchers to develop and study crowdsourced and point-of-care data for understanding infectious and chronic disease in populations worldwide.

Ideal postdoctoral candidates will have a Ph.D. with a strong background in bioinformatics, biostatistics, computer science or related field. Expertise in statistical machine learning and/or data mining are required. Preferred requirements for this position include experience designing software applications and/or storing, retrieving, and analyze large datasets. Experience with R, Python, SQL, JavaScript is preferred. Experience in hacking with cloud technologies (e.g., AWS, Hadoop) is a big plus. You must demonstrate an interest or experience in working with biological data such as genomic sequence, syndromic surveillance or physiological data.

This is an exciting research area and New York City provides great opportunities for networking and support of innovative work. Our group is engaged in many high-profile studies in collaboration with startups and other groups. The selected post-doc will be supported and encouraged to generate high impact publications, gain experience in supervising students and in grant writing if interested. All applicants should send an updated CV to Rumi Chunara (rumi.chunara@nyu.edu).

ISIT 2015 : statistics and learning

Posted on by

The advantage of flying to Hong Kong from the US is that the jet lag was such that I was actually more or less awake in the mornings. I didn’t take such great notes during the plenaries, but they were rather enjoyable, and I hope that the video will be uploaded to the ITSOC website soon.

There were several talks on entropy estimation in various settings that I did not take great notes on, to wit:

  • OPTIMAL ENTROPY ESTIMATION ON LARGE ALPHABETS VIA BEST POLYNOMIAL APPROXIMATION (Yihong Wu, Pengkun Yang, University Of Illinois, United States)
  • DOES DIRICHLET PRIOR SMOOTHING SOLVE THE SHANNON ENTROPY ESTIMATION PROBLEM? (Yanjun Han, Tsinghua University, China; Jiantao Jiao, Tsachy Weissman, Stanford University, United States)
  • ADAPTIVE ESTIMATION OF SHANNON ENTROPY (Yanjun Han, Tsinghua University, China; Jiantao Jiao, Tsachy Weissman, Stanford University, United States)

I would highly recommend taking a look for those who are interested in this problem. In particular, it looks like we’re getting towards more efficient entropy estimators in difficult settings (online, large alphabet), which is pretty exciting.

QUICKEST LINEAR SEARCH OVER CORRELATED SEQUENCES
Javad Heydari, Ali Tajer, Rensselaer Polytechnic Institute, United States
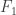This talk was about hypothesis testing where the observer can control the samples being taken by traversing a graph. We have an n-node graph (c.f. a graphical model) representing the joint distribution on n variables. The data generated is i.i.d. across time according to either F_0 or F_1. At each time you get to observe the data from only one node of the graph. You can either observe the same node as before, explore by observing a different node, or make a decision about whether the data from from F_0 or F_1. 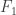By adopting some costs for different actions you can form a dynamic programming solution for the search strategy but it’s pretty heavy computationally. It turns out the optimal rule for switching has a two-threshold structure and can be quite a bit different than independent observations when the correlations are structured appropriately.

MISMATCHED ESTIMATION IN LARGE LINEAR SYSTEMS
Yanting Ma, Dror Baron, North Carolina State University, United States; Ahmad Beirami, Duke University, United States
The mismatch studied in this paper is a mismatch in the prior distribution for a sparse observation problem y = Ax + \sigma_z z, where x \sim P (say a Bernoulli-Gaussian prior). The question is what happens when we do estimation assuming a different prior Q. The main result of the paper is an analysis of the excess MSE using a decoupling principle. Since I don’t really know anything about the replica method (except the name “replica method”), I had a little bit of a hard time following the talk as a non-expert, but thankfully there were a number of pictures and examples to help me follow along.

SEARCHING FOR MULTIPLE TARGETS WITH MEASUREMENT DEPENDENT NOISE
Yonatan Kaspi, University of California, San Diego, United States; Ofer Shayevitz, Tel-Aviv University, Israel; Tara Javidi, University of California, San Diego, United States
This was another search paper, but this time we have, say, K targets W_1, W_2, \ldots, W_K uniformly distributed in the unit interval, and what we can do is query at each time n a set S_n \subseteq [0,1] and get a response Y_n = X_n \oplus Z_n where X_n = \mathbf{1}( \exists W_k \in S_n ) and Z_n \sim \mathrm{Bern}( \mu(S_n) + b ) where \mu is the Lebesgue measure. So basically you can query a set and you get a noisy indicator of whether you hit any targets, where the noise depends on the size of the set you query. At some point \tau you stop and guess the target locations. You are (\epsilon,\delta) successful if the probability that you are within \delta of each target is less than \epsilon. The targeting rate is the limit of \log(1/\delta) / \mathbb{E}[\tau] as \epsilon,\delta \to 0 (I’m being fast and loose here). Clearly there are some connections to group testing and communication with feedback, etc. They show there is a significant gap between the adaptive and nonadaptive rate here, so you can find more targets if you can adapt your queries on the fly. However, since rate is defined for a fixed number of targets, we could ask how the gap varies with K. They show it shrinks.

ON MODEL MISSPECIFICATION AND KL SEPARATION FOR GAUSSIAN GRAPHICAL MODELS
Varun Jog, University of California, Berkeley, United States; Po-Ling Loh, University of Pennsylvania, United States
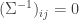The graphical model for jointly Gaussian variables has no edge between nodes i and j if the corresponding entry (\Sigma^{-1})_{ij} = 0 in the inverse covariance matrix. They show a relationship between the KL divergence of two distributions and their corresponding graphs. The divergence is lower bounded by a constant if they differ in a single edge — this indicates that estimating the edge structure is important when estimating the distribution.

CONVERSES FOR DISTRIBUTED ESTIMATION VIA STRONG DATA PROCESSING INEQUALITIES
Aolin Xu, Maxim Raginsky, University of Illinois at Urbana–Champaign, United States
Max gave a nice talk on the problem of minimizing an expected loss \mathbb{E}[ \ell(W, \hat{W}) ] of a d-dimensional parameter W which is observed noisily by separate encoders. Think of a CEO-style problem where there is a conditional distribution P_{X|W} such that the observation at each node is a d \times n matrix whose columns are i.i.d. and where the j-th row is i.i.d. according to P_{X|W_j}. Each sensor gets independent observations from the same model and can compress its observations to b bits and sends it over independent channels to an estimator (so no MAC here). The main result is a lower bound on the expected loss as s function of the number of bits latex b, the mutual information between W and the final estimate \hat{W}. 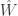The key is to use the strong data processing inequality to handle the mutual information — the constants that make up the ratio between the mutual informations is important. I’m sure Max will blog more about the result so I’ll leave a full explanation to him (see what I did there?)

More on Shannon theory etc. later!

AISTATS 2015: a few talks from one day

Posted on by

I attended AISTATS for about a day and change this year — unfortunately due to teaching I missed the poster I had there but Shuang Song presented a work on learning from data sources of different quality, which her work with Kamalika Chaudhuri and myself. This was my first AISTATS. It had single track of oral presentations and then poster sessions for the remaining papers. The difficulty with a single track for me is that my interest in the topics is relatively focused, and the format of a general audience with a specialist subject matter meant that I couldn’t get as much out of the talks as I would have wanted. Regardless, I did get exposed to a number of new problems. Maybe the ideas can percolate for a while and inform something in the future.

Computational Complexity of Linear Large Margin Classification With Ramp Loss
Søren Frejstrup Maibing, Christian Igel
The main result of this paper (I think) is that ERM under ramp loss is NP-hard. They gave the details of the reduction but since I’m not a complexity theorist I got a bit lost in the weeds here.

A la Carte — Learning Fast Kernels
Zichao Yang, Andrew Wilson, Alex Smola, Le Song
Ideas like “random kitchen sinks” and other kernel approximation methods require you to have a kernel you want to approximate, but in many problems you in fact need to learn the kernel from the data. If I give you a kernel function k(x,x') = k( |x - x'| ), then you can take the Fourier transform K(\omega) of k. This turns out to be a probability distribution, so you can sample random \{\omega_i\} i.i.d. and build a randomized Fourier approximation of k. If you don’t know the kernel function, or you have to learn it, then you could instead try to learn/estimate the transform directly. This paper was about trying to do that in a reasonably efficient way.

Learning Where to Sample in Structured Prediction
Tianlin Shi, Jacob Steinhardt, Percy Liang
This was about doing Gibbs sampling, not for MCMC sampling from the stationary distribution, but for “stochastic search” or optimization problems. The intuition was that some coordinates are “easier” than others, so we might want to focus resampling on the harder coordinates. But this might lead to inaccurate sampling. The aim here twas to build a heterogenous sampler that is cheap to compute and still does the right thing.

Tradeoffs for Space, Time, Data and Risk in Unsupervised Learning
Mario Lucic, Mesrob Ohannessian, Amin Karbasi, Andreas Krause
This paper won the best student paper award. They looked at a k-means problem where they do “data summarization” to make the problem a bit more efficient — that is, by learning over an approximation/summary of the features, they can find different tradeoffs between the running time, risk, and sample size for learning problems. The idea is to use coresets — I’d recommend reading the paper to get a better sense of what is going on. It’s on my summer reading list.

Averaged Least-Mean-Squares: Bias-Variance Trade-offs and Optimal Sampling Distributions
Alexandre Defossez, Francis Bach
What if you want to do SGD but you don’t want to sample the points uniformly? You’ll get a bias-variance tradeoff. This is another one of those “you have to read the paper” presentations. A nice result if you know the background literature, but if you are not a stochastic gradient aficionado, you might be totally lost.

Sparsistency of \ell_1-Regularized M-Estimators
Yen-Huan Li, Jonathan Scarlett, Pradeep Ravikumar, Volkan Cevher
In this paper they find a new condition, which they call local structured smoothness, which is sufficient for certain M-estimators to be “sparsistent” — that is, they recover the support pattern of a sparse parameter asymptotically as the number of data points goes to infinity. Examples include the LASSO, regression in general linear models, and graphical model selection.

Some of the other talks which were interesting but for which my notes were insufficient:

  • Two-stage sampled learning theory on distributions (Zoltan Szabo, Arthur Gretton, Barnabas Poczos, Bharath Sriperumbudur)
  • Generalized Linear Models for Aggregated Data (Avradeep Bhowmik, Joydeep Ghosh, Oluwasanmi Koyejo)
  • Efficient Estimation of Mutual Information for Strongly Dependent Variables (Shuyang Gao, Greg Ver Steeg, Aram Galstyan)
  • Sparse Submodular Probabilistic PCA (Rajiv Khanna, Joydeep Ghosh, Russell Poldrack, Oluwasanmi Koyejo)

Signal boost: Postdoc in Privacy at Penn State

Posted on by

Sofya Raskhodnikova and Adam Smith are looking to fill a postdoc position at Penn State for a multi-year project on privacy, streaming and learning.

Qualifications: Ph.D., with expertise in the theoretical foundations of at least one of the research areas (algorithms, machine learning and statistics, data privacy). Willingness to work on a cross-disciplinary project.

More about the project leaders: Sofya Raskhodnikova, Adam Smith.

Duration and compensation: At least one year, renewable. Start date is
negotiable, though we slightly prefer candidates starting fall 2015. Salary is competitive.

Applicants should email a CV, short research statement and list of references directly to the project leaders ({asmith,sofya}@cse.psu.edu) with “postdoc” in the subject line.

Location: The university is located in the beautiful college town of
State College in the center of Pennsylvania. The State College area has 130,000 inhabitants and offers a wide variety of cultural and outdoor recreational activities. The university offers outstanding events from collegiate sporting events to fine arts productions. Many major population centers on the east coast (New York, Philadelphia, Pittsburgh, Washington D.C., Baltimore) are only a few hours’ drive away and convenient air services to several major hubs are operated by three major airlines out of State College.

Penn State is an equal opportunity employer. We encourage applications from underrepresented minorities.

ITA 2015: quick takes

Posted on by

Better late than never, I suppose. A few weeks ago I escaped the cold of New Jersey to my old haunts of San Diego. Although La Jolla was always a bit fancy for my taste, it’s hard to beat a conference which boasts views like this:

A view from the sessions at ITA 2015

A view from the sessions at ITA 2015


I’ll just recap a few of the talks that I remember from my notes — I didn’t really take notes during the plenaries so I don’t have much to say about them. Mostly this was due to laziness, but finding the time to blog has been challenging in this last year, so I think I have to pick my battles. Here’s a smattering consisting of

\{ \mathrm{talks\ attended} \} \cap \{ \mathrm{talks\ with\ understandable\ notes} \}

(Information theory)
Emina Soljanin talked about designing codes that are good for fast access to the data in distributed storage. Initial work focused on how to repair codes under disk failures. She looked at how easy it is to retrieve the information afterwords to guarantee some QoS for the storage system. Adam Kalai talked about designing compression schemes that work for an “audience” of decoders. The decoders have different priors on the set of elements/messages so the idea is to design an encoder that works for this ensemble of decoders. I kind of missed the first part of the talk so I wasn’t quite sure how this relates to classical work in mismatched decoding as done in the information theory world. Gireeja Ranade gave a great talk about defining notions of capacity/rate need to control a system which as multiplicative uncertainty. That is, x[n+1] = x[n] + B[n] u[n] where B[n] has the uncertainty. She gave a couple of different notions of capacity, relating to the ratio | x[n]/x[0] | — either the expected value of the square or the log, appropriately normalized. She used a “deterministic model” to give an explanation of how control in this setting is kind of like controlling the number of significant bits in the state: uncertainty increases this and you need a certain “amount” of control to cancel that growth.

(Learning and statistics)
I learned about active regression approaches from Sivan Sabato that provably work better than passive learning. The idea there is do to use a partition of the X space and then do piecewise constant approximations to a weight function that they use in a rejection sampler. The rejection sampler (which I thought of as sort of doing importance sampling to make sure they cover the space) helps limit the number of labels requested by the algorithm. Somehow I had never met Raj Rao Nadakuditi until now, and I wish I had gotten a chance to talk to him further. He gave a nice talk on robust PCA, and in particular how outliers “break” regular PCA. He proposed a combination of shrinkage and truncation to help make PCA a bit more stable/robust. Laura Balzano talked about “estimating subspace projections from incomplete data.” She proposed an iterative algorithm for doing estimation on the Grassmann manifold that can do subspace tracking. Constantine Caramanis talked about a convex formulation for mixed regression that gives a guaranteed solution, along with minimax sample complexity bounds showing that it is basically optimal. Yingbin Liang talked about testing approaches for understanding if there is an “anomalous structure” in a sequence of data. Basically for a sequence Y_1, Y_2, \ldots, Y_n, the null hypothesis is that they are all i.i.d. \sim p and the (composite) alternative is that there an interval of indices which are \sim q instead. She proposed a RKHS-based discrepancy measure and a threshold test on this measure. Pradeep Ravikumar talked about a “simple” estimator that was a “fix” for ordinary least squares with some soft thresholding. He showed consistency for linear regression in several senses, competitive with LASSO in some settings. Pretty neat, all said, although he also claimed that least squares was “something you all know from high school” — I went to a pretty good high school, and I don’t think we did least squares! Sanmi Koyejo talked about a Bayesian devision theory approach to variable selection that involved minimizing some KL-divergence. Unfortunately, the resulting optimization ended up being NP-hard (for reasons I can’t remember) and so they use a greedy algorithm that seems to work pretty well.

(Privacy)
Cynthia Dwork gave a tutorial on differential privacy with an emphasis on the recent work involving false discovery rate. In addition to her plenary there were several talks on differential privacy and other privacy measures. Kunal Talwar talked about their improved analysis of the SuLQ method for differentially private PCA. Unfortunately there were two privacy sessions in parallel so I hopped over to see John Duchi talk about definitions of privacy and how definitions based on testing are equivalent to differential privacy. The testing framework makes it easier to prove minimax bounds, though, so it may be a more useful view at times. Nadia Fawaz talked about privacy for time-series data such as smart meter data. She defined different types of attacks in this setting and showed that they correspond to mutual information or directed mutual information, as well as empirical results on a real data set. Raef Bassily studied a estimation problem in the streaming setting where you want to get a histogram of the most frequent items in the stream. They reduce the problem to one of finding a “unique heavy hitter” and develop a protocol that looks sort of like a code for the MAC: they encode bits into a real vector, had noise, and then add those up over the reals. It’s accepted to STOC 2015 and he said the preprint will be up soon.

Fenchel duality, entropy, and the log partition function

Posted on by

[Update: As Max points out in the comments, this is really a specialized version of the Donsker-Varadhan formula, also mentioned by Mokshay in a comment here. I think the difficulty with concepts like these is that they are true for deeper reasons than the ones given when you learn them — this is a special case that requires undergraduate probability and calculus, basically.]

One of my collaborators said to me recently that it’s well known that the “negative entropy is the Fenchel dual of the log-partition function.” Now I know what these words meant, but it somehow was not a fact that I had learned elsewhere, and furthermore, a sentence like that is frustratingly terse. If you already know what it means, then it’s a nice shorthand, but for those trying to figure it out, it’s impenetrable jargon. I tried running it past a few people here who are generally knowledgeable but are not graphical model experts, and they too were unfamiliar with it. While this is just a simple thing about conjugate duality, I think it doesn’t really show up in information theory classes unless the instructor talks a bit more about exponential family distributions, maximum entropy distributions, and other related concepts. Bert Huang has a post on Jensen’s inequality as a justification.

We have a distribution in the exponential family:

p(x; \theta) = \exp( \langle \theta, \phi(x) \rangle - A(\theta) )

As a side note, I often find that the exponential family is not often covered in systems EE courses. Given how important it is in statistics, I think it should be a bit more of a central concept — I’m definitely going to try and work it in to the detection and estimation course.

For the purposes of this post I’m going to assume x takes values in a discrete alphabet \mathcal{X} (say, n-bit strings). The function \phi(x) is a vector of statistics calculated from x, and \theta is a vector of parameters. the function A(\theta) is the log partition function:

A(\theta) = \log\left( \sum_{x} \exp( \langle \theta, \phi(x) \rangle ) \right)

Where the partition function is

Z(\theta) = \sum_{x} \exp( \langle \theta, \phi(x) \rangle )

The entropy of the distribution is easy to calculate:

H(p) = \mathbb{E}[ - \log p(x; \theta) ] = A(\theta) - \langle \theta, \mathbb{E}[\phi(x)] \rangle

The Fenchel dual of a function f(\theta) is the function

g(\psi) = \sup_{\theta} \left\{ \langle \psi, \theta \rangle - f(\theta) \right\}.

So what’s the Fenchel dual of the log partition function? We have to take the gradient:

\nabla_{\theta} \left( \langle \psi, \theta \rangle - A(\theta) \right) = \psi - \frac{1}{Z(\theta)} \sum_{x} \exp( \langle \theta, \phi(x) \rangle ) \phi(x) = \psi - \mathbb{E}[ \phi(x) ]

So now setting this equal to zero, we see that at the optimum \theta^*:

\langle \psi, \theta^* \rangle = \langle \mathbb{E}[ \phi(x) ], \theta^* \rangle

And the dual function is:

g(\psi) = \langle \mathbb{E}[ \phi(x) ], \theta^* \rangle - A(\theta^*) = - H(p)

The standard approach seems to go the other direction by computing the dual of the negative entropy, but that seems more confusing to me (perhaps inspiring Bert’s post above). Since the log partition function and negative entropy are both convex, it seems easier to exploit the duality to prove it in one direction only.