After seeing Nisim’s ISIT talk on LP Decoding of Regular LDPC Codes in Memoryless Channels, I remembered one issue that has been puzzling me for a while: if there are any explicit constructions of LDPC codes that have a provable nonzero threshold (for block-error probability, hence excluding density evolution arguments) i.e. correct a constant fraction of bit-flipping errors (other channels would be harder)– under any efficient decoder.
The question seems trivial: As is well-known, a random 
regular graph will be a very high quality expander (for very small sets) and therefore a (very small) constant fraction of bit-flipping errors can be corrected by Sipser & Spielman‘s bit flipping algorithm.
regular graph will be a very high quality expander (for very small sets) and therefore a (very small) constant fraction of bit-flipping errors can be corrected by Sipser & Spielman‘s bit flipping algorithm.Also the work by Feldman et al. LP decoding corrects a constant fraction of errors establishes correction of an adversarial set of bit-flipping errors for expander graphs under LP decoding.
But here is the catch: sure, a random graph is a good expander with high probability, but how do we check if a given graph is a good expander?
The key of course is my definition of explicit construction: I mean an algorithm that terminates in polynomial time and gives me a code that certifiably works (and I think this is relevant to practice, since at the end of the day I have to use one fixed code). The only efficient way that I know to check expansion involves spectral methods ( This is from Modern Coding theory by Richardson & Urbanke) : If we have a regular bipartite graph with 
variable nodes and 
check nodes, if we take 
to be the incidence matrix of the bipartite graph (the parity check matrix of the code), we can form 
and look at its eigenvalues
regular bipartite graph with variable nodes and check nodes, if we take to be the incidence matrix of the bipartite graph (the parity check matrix of the code), we can form 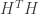and look at its eigenvalues
and Tanner’s spectral bound on expansion is that expansion 
is greater than
for any size of expanding sets $\alpha$. Unfortunately this bound cannot certify expansion for any 
, which is exactly the point where it starts being useful for coding theory. Perhaps there are stronger spectral bounds that could establish more expansion, the book Spectral Graph Theory by Fan Chung Graham contains a lot of material on that point but I have not seen any such applications to coding.So ok, lets say we do not know how to construct (or certify) that LDPCs have high expansion, how about other graph properties that will guarantee a correctable fraction of errors in polynomial time? This started when I was working with Costas on LP decoding for LDPC codes and we were always (incorrectly) assuming that random regular bipartite graphs will have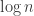 
girth with high probability. When we actually tried to find a proof for this, for example looking at the Modern Coding theory book we find that usual proofs establish a significantly weaker statement: in a random regular graph, if you start from a variable and start expanding the tree, you will not loop around after a constant number of steps with 
probability. This is what is refered to as ‘locally-tree like’. I do not know of any stronger statements but I think it can be easily shown that for any fixed cycle length, the expected number of cycles of that length is constant for regular random graphs.
girth with high probability. When we actually tried to find a proof for this, for example looking at the Modern Coding theory book we find that usual proofs establish a significantly weaker statement: in a random regular graph, if you start from a variable and start expanding the tree, you will not loop around after a constant number of steps with probability. This is what is refered to as ‘locally-tree like’. I do not know of any stronger statements but I think it can be easily shown that for any fixed cycle length, the expected number of cycles of that length is constant for regular random graphs.The breakthrough paper by Arora, Daskalakis and Steurer, ‘Message-Passing Algorithms and Improved LP Decoding‘ establishes that regular LDPCs with 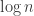girth will correct a constant fraction of random bit-flipping errors whp under LP decoding. But how do we find regular LDPCs with girth ?
girth will correct a constant fraction of random bit-flipping errors whp under LP decoding. But how do we find regular LDPCs with 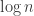girth ?After searching a little I found the recent work of Bayati et al.
Generating Random Graphs with Large Girth and Generating random Tanner-graphs with large girth that talk about the related problem of generating a graph with high girth uniformly from all such graphs (and with a given degree distribution) but as far as I understood these constructions cannot guarantee a diameter scaling like 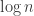(but only any constant diameter). This is of course the relevant practical question but the scaling issue remains.
(but only any constant diameter). This is of course the relevant practical question but the scaling issue remains.The only construction that I know is the one found in the appendix of Gallager’s thesis that contains a deterministic algorithm that constructs regular Tanner graphs with girth.
regular Tanner graphs with 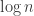girth.The same question is relevant for compressed sensing when we ask for sparsity in the measurement matrix: All the constructions that I know for sparse measurement matrices (that require the optimal number of measurements under Basis pursuit, e.g. see the survey of Gilbert and Indyk: Sparse Recovery using Sparse Matrices) are constructed from high 
bipartite expander graphs. But given a fixed measurement matrix how do we certify that it is good and should be implemented in a system?
bipartite expander graphs. But given a fixed measurement matrix how do we certify that it is good and should be implemented in a system?Of course one can use Message passing algorithms for compressed sensing (by Donoho, Maleki and Montanari) and obtain sparse measurement matrices with very good thresholds but under a different decoding algorithm.
The close connection of compressed sensing (under LP – Basis pursuit decoding) and channel coding (under LP decoding) gives one path for certifiable measurement matrices that are sparse):
1. The Arora, Daskalakis & Steurer paper guarantees that (3,6) regular graphs with 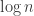girth correct a (quite high– much higher than expansion arguments) constant fraction of errors under LP decoding.
girth correct a (quite high– much higher than expansion arguments) constant fraction of errors under LP decoding.2. Gallager’s thesis appendix contains deterministic constructions of such (3,6) regular sparse matrices.
3. Our connection result establishes that if a matrix corrects a constant fraction of bit flipping errors, the same matrix used as a compressed sensing measurement matrix will recover all sparse signals (of the same support as the bit-flipping errors).
Combining (1)+(2)+(3) we obtain that: for sensing a length signal with 
measurements one recovers almost all sparse signals of size up to $0.05 n$ (whp over supports) and the 
measurement matrix has 
non-zeros. (see our recent paper )
signal with measurements one recovers almost all sparse signals of size up to $0.05 n$ (whp over supports) and the measurement matrix has 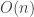non-zeros. (see our recent paper )Conclusion: The Appendix C in Gallager’s thesis contains the best sparse compressed sensing measurement matrices known (under basis pursuit).
Not bad for 1963!
An Ergodic Walk 
In the mathematics community, it is well known that construction of large-girth graphs is non-trivial. There are a lot of Cayley graph based constructions. Besides, I think it’s an open secret that Gallager’s algorithm Appendix C is flawed.
Really? What is the flaw? Perhaps I’ll need to study this in more detail. Also do you know of any other construction with logn girth?
The LPS ramanujan graphs have girth that goes as logn …
I would be very interested in knowing what the flaw in Gallager proof is. Any pointers?
There are constructions by Lazebnik, Ustimenko, and Wolder (see http://www.math.udel.edu/~lazebnik/papers/RSG5.ps), and those are the only other constructions that I am aware of. We have some recent constructions that are better, but really, I think the issue has not gotten the attention that it deserves.
Gallager’s construction has something called the “emergency procedure.” I’m not convinced that emergency procedure works all the time. There is a proof for this claim in the appendix. I think there are some obvious mistakes in the proof. If somebody can fix those, that’ll be great. Btw, try to get the original monograph published by MIT press. MacKay’s homepage has a LaTeX version has quite a few typos in Appendix C.
Constructing log n girth regular graphs (regular in graph theoretic sense, not in LDPC code sense) is something studied well by the Math research community. Some of the papers by Biggs can be a good starting point for what the mathematicians have figured out.
“Constructing log n girth regular graphs (regular in graph theoretic sense, not in LDPC code sense) is something studied well by the Math research community. ”
Yes! The concept of a “cage-graph” is very useful here: these are graphs of minimum number of nodes for a given girth. Cages are known for very few values of girth g, but upper and lower bounds on the number of nodes have been studied for quite a while (see http://www.combinatorics.org/Surveys/ds16.pdf for a very nice survey).
As I mentioned in the last comment, this led Lazebnik, Ustimenko and Woldar to consider bi-regular bi-partite constructions (which is what LDPC code-graphs are) : http://www.math.udel.edu/~lazebnik/papers/RSG5.ps .
In our CISS paper this year (see Section IV of http://www.eecs.berkeley.edu/~pulkit/files/WireLength.pdf ), we use constructions for regular (cage-y) graphs to construct bipartite graphs that are (to my surprise) smaller than those of Lazebnik et al. This is why I believe that the problem hasn’t received the attention it deserves.
Just to be precise, the goal here is to obtain a construction for any g that gives an upper bound in closed form (as a function of g). There are many, many constructions that are algorithmic, but without analytical upper bounds, it is difficult to use these constructions for understanding the scaling of graph size with g. (for example, for getting an asymptotic understanding of required wire-lengths on decoding chips, something we explore in the CISS paper).