I started reading Convex Games in Banach Spaces, by Sridharan and Tewari and then got interested in the work of G. Pisier on martingales in Banach spaces, which studies how probability and geometry interact. Some of the definitions differ a bit between these papers (the former does things in terms of martingale difference sequences).
A Banach space 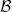 has Martingale-type
has Martingale-type  (or M-type
(or M-type  ) if there is a constant
) if there is a constant 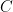 such that for any
such that for any  and
and 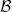 -valued martingale
-valued martingale  , we have
, we have
![\displaystyle \sup_{t} \mathop{\mathbb E}\left[ \left\| Y_t \right\| \right] \le C \left( \sum_{t=1}^{\infty} \mathop{\mathbb E}[ \left\| Y_t - Y_{t-1} \right\| ^p ] \right)^{1/p}.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%09%5Csup_%7Bt%7D+%5Cmathop%7B%5Cmathbb+E%7D%5Cleft%5B+%5Cleft%5C%7C+Y_t+%5Cright%5C%7C+%5Cright%5D+%5Cle+C+%5Cleft%28+%5Csum_%7Bt%3D1%7D%5E%7B%5Cinfty%7D+%5Cmathop%7B%5Cmathbb+E%7D%5B+%5Cleft%5C%7C+Y_t+-+Y_%7Bt-1%7D+%5Cright%5C%7C+%5Ep+%5D+%5Cright%29%5E%7B1%2Fp%7D.+%09&bg=ffffff&fg=000000&s=0&c=20201002)
A Banach space 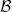 has Martingale-cotype
has Martingale-cotype  (or M-cotype
(or M-cotype  ) if there is a constant
) if there is a constant 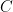 such that for any
such that for any  and
and 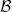 -valued martingale
-valued martingale  , we have
, we have
![\displaystyle \left( \sum_{t=1}^{\infty} \mathop{\mathbb E}[ \left\| Y_t - Y_{t-1} \right\|^q ] \right)^{1/q} \le C \sup_{t} \mathop{\mathbb E}\left[ \left\| Y_t \right\| \right].](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%09+%5Cleft%28+%5Csum_%7Bt%3D1%7D%5E%7B%5Cinfty%7D+%5Cmathop%7B%5Cmathbb+E%7D%5B+%5Cleft%5C%7C+Y_t+-+Y_%7Bt-1%7D+%5Cright%5C%7C%5Eq+%5D+%5Cright%29%5E%7B1%2Fq%7D+%09+%5Cle+%09+C+%5Csup_%7Bt%7D+%5Cmathop%7B%5Cmathbb+E%7D%5Cleft%5B+%5Cleft%5C%7C+Y_t+%5Cright%5C%7C+%5Cright%5D.+%09&bg=ffffff&fg=000000&s=0&c=20201002)
So far these are statements about how martingales behave in these spaces, and you can see a little geometry in the  kind of stuff, but how does this relate to overall geometric properties of the space?
kind of stuff, but how does this relate to overall geometric properties of the space?
A Banach space 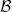 is reflexive if it is isomorphic to its double dual (the dual of its dual space). The space
is reflexive if it is isomorphic to its double dual (the dual of its dual space). The space 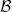 is reflexive if and only if its dual
is reflexive if and only if its dual 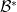 is reflexive. A space
is reflexive. A space 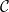 is finitely representable in
is finitely representable in 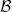 if for any
if for any  and any
and any  there exists an isomorphism
there exists an isomorphism 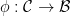 such that
such that

A Banach space 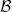 is super-reflexive if no non-reflexive Banach space is finitely representable in
is super-reflexive if no non-reflexive Banach space is finitely representable in 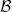 . A result of James shows that a space is super-reflexive if and only if its dual is super-reflexive. Reflexivity means a space is “nice” and super-reflexivity is a kind of “uniform niceness.”
. A result of James shows that a space is super-reflexive if and only if its dual is super-reflexive. Reflexivity means a space is “nice” and super-reflexivity is a kind of “uniform niceness.”
The norm for a Banach space is uniformly convex if for every 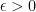 there exists a
there exists a 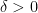 such that for two unit vectors
such that for two unit vectors  and
and 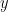 ,
,

implies

For example, for 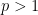 the spaces
the spaces 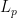 and
and  are uniformly convex. Another way to picture it is that if the midpoint of the chord between
are uniformly convex. Another way to picture it is that if the midpoint of the chord between  and
and 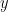 is close to the surface of the unit ball, then the chord has to be short. Per Enflo showed that if a Banach space
is close to the surface of the unit ball, then the chord has to be short. Per Enflo showed that if a Banach space 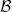 is super-reflexive, it has an equivalent norm which is uniformly convex.
is super-reflexive, it has an equivalent norm which is uniformly convex.
It turns out that the M-type is related to the degree of convexity of a space, namely how uniformly convex the norm is (and in turn connected to super-reflexivity). A space is  –uniformly convex if
–uniformly convex if

Gilles Pisier made the connection to M-types : a Banach space is super-reflexive if and only if it has M-type 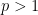 (or M-cotype
(or M-cotype  ). Furthermore, a Banach space has M-cotype
). Furthermore, a Banach space has M-cotype  if and only if
if and only if 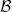 has a
has a  -uniformly convex norm.
-uniformly convex norm.
So the big picture is this: super-reflexivity is enough to guarantee a uniformly convex norm, but the M-cotype characterizes the degree of how convex that norm is.
References:
Sridharan, Kartik and Tewari, Ambuj, Convex Games in Banach Spaces, Proceedings of COLT, 2010.
Enflo, Per, Banach spaces which can be given an equivalent uniformly convex norm, Israel Journal of Mathematics 13 (1972), 281-288.
James, Robert C., Super-reflexive Banach spaces., Canadian Journal of Mathematics 24 (1972), 896Ð904.
Pisier, Gilles, Probabilistic Methods in the Geometry of Banach spaces, in G. Letta and M. Pratelli, ed., Probability and Analysis, v.1206 of Lecture Notes in Mathematics, p167–241, Springer, 1986.
Pisier, Gilles, Martingales with values in uniformly convex spaces, Israel Journal of Mathematics 20 (1975), no. 3-4, 326Ð350.
Pisier, Gilles, Martingales in Banach Spaces (in connection with Type and Cotype), IHP Winter Course online lecture notes, 2011.
Lovaglia, A. R., Locally uniformly convex Banach spaces, Trans. Amer. Math. Soc. 78, (1955). 225Ð238.