Tag Archives: probability

The card-cyclic to random shuffle

Posted on by

I heard about this cool-sounding seminar at the Berkeley Statistics department:

Mixing time of the card-cyclic to random shuffle
Ben Morris

We analyze the following method for shuffling n cards. First, remove card 1 (i.e., the card with label 1) and then re-insert it randomly into the deck. Then repeat with cards 2, 3,…, n. Call this a round. R. Pinsky showed, somewhat surprisingly, that the mixing time is greater than one round. We show that in fact the mixing time is on the order of \log n rounds.

The talk is based on a paper with Weiyang Ning (a student at UW) and Yuval Peres. The description the results is somewhat different because it’s \log n rounds of n moves, or n \log n moves. From the intro to the paper:

To prove the lower bound we introduce the concept of a barrier between two parts of the deck that moves along with the cards as the shuffling is performed. Then we show that the trajectory of this barrier can be well-approximated by a deterministic function f… we relate the mixing rate of the chain to the rate at which f converges to a constant.

The key is to use path coupling, a technique pioneered by Bubley and Dyer. It’s a cute result and would be a fun paper to read for a class project or something, I bet.

Strategies in the Iterated Prisoner’s Dilemma

Posted on by

Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent
William H. Press and Freeman J. Dyson
PNAS 109(26), June 26, 2012

This was an interesting little paper that I learned about that I am still digesting; as I’ve said before, I’m not a game theory guy. They start out with a 2×2 game, the classical Prisoner’s Dilemma with players X and Y — if both cooperate (C), they payoffs are (R,R), if the first (resp. second) defects (D) they are (T,S) (resp. (S,T)) and if they both defect then (P,P). The usual conditions are T > R > P > S to keep it interesting.

In an iterated game the players get to play over and over again and try to develop strategies to win more than their opponent. The first interesting (to me) observation in this paper is that strategies which maintain a long memory are dominated by those which maintain a short memory in the sense that if for any long-memory strategy of Y, the payoff for a short-memory strategy of X is the same as a certain short-memory strategy of Y. So if your opponent is playing a short-memory strategy you should also play a similar short-memory strategy.

So with that idea in mind they look at first-order Markov strategies — given the past state (CC, CD, DC, DD) player X randomly chooses whether to cooperate or not in the next round. Thus the problem is specified by 4 conditional probabilities of cooperating conditioned on the previous state, and you can compute a 4×4 Markov matrix of transition probabilities out of the randomized strategies of each player.

Now the game becomes how they payoffs behave under different choices of strategy, which boil down to spectral / structural properties of this Markov matrix. To be honest, I found the discussion in the rest of the paper more confusing than enlightening because the mathematics was a little obscured by the discussion of implications. I realize this is a PNAS paper but it felt a little discursive at times and the mathematical intuition was not entirely clear to me.

Still, it’s a short read and probably worth a peruse.

Thresholds in random integer programs

Posted on by

Karthik Chandrasekaran gave a talk at TTI today on the feasibility of integer programs. Given a polytope defined by the inequalities A x \le b in dimension n, can we say whether the polytope contains an integer point? In general, the problem is NP-hard, but efficient algorithms are known for special sub-cases. The goal in this talk was to understand if random instances of the problem are also hard.

The first thing to figure out is what do we mean by a random instance? Consider a point x_0 and the sphere S of radius R around x_0. Now draw m vectors x_1, x_2, \ldots, x_m uniformly from the surface of the unit sphere, and consider the polytope defined by faces which are tangent to S at x_0 + x_i for i = 1, 2, \ldots, m. That is, the vector x_0 + x_i is the normal vector of that face. This defines a random polytope whose distribution depends on the parameters (n,m,x_0,R). The goal is to find how R scales with n and m such that with high probability, the polytope contains an integer point for all x_0.

If the radius R is too small, then this will be hard to do because guaranteeing that an integer point is in the interior for all x_0 becomes hard. If R = \sqrt{n}/2, then we will always have an integer point. What should the real scaling for R look like?

The simple form of the main result is that if n \le m \le 2^{\sqrt{n}} and R \ge c_1 \sqrt{log(m/n)}, with high probability the polytope will have an integer point for every x_0. Conversely, if R \le c_0 \sqrt{ log(m/n) }, then with high probability the polytope “centered” at x_0 = (1/2,1/2,\ldots,1/2) with not contain an integer point. Note that if the number of faces is linear in n, then a constant radius is sufficient. I’m trying to square that with the “infinite dimensional spheres have vanishing volume and expanding surface area” but I think the fact that the polytope is “pointy” means that L_1 geometry gives better intuition.

To prove these bounds on R, they make a connection to the discrepancy of random Gaussian matrices (which approximate the random unit vector row matrices). The paper is on arxiv for those who want to take a look.

Cover’s test for the irrationality of a coin

Posted on by

Someone hands you a coin which has a probability p of coming up heads. You can flip the coin as many times as you like (or more precisely, you can flip the coin an infinite number of times). Let S = \{r_i : i = 1, 2, \ldots\} be the set of rational numbers in [0,1]. After each flip, you have to guess one of the following hypotheses: that p = r_i for a particular i, or p is irrational. Furthermore, you can only make a finite number of errors for any p \in [0,1] - N_0, where N_0 is a set of irrationals of Lebesgue measure 0. Can you do it? If so, how?

This is the topic addressed by a pair of papers that Avrim Blum mentioned in Yoav Freund‘s remembrances of Tom Cover:

COVER, THOMAS M (1973). On determining the irrationality of the mean of a random variable. Ann. Math. Statist. 1862-871.
COVER & HIRSCHLER (1975). A finite memory test of the irrationality of the parameter of a coin. Annals of Statistics, 939-946

I’ll talk about the first paper in this post.

The algorithm is not too complicated — you basically go in stages. For each time j = 1, 2, \ldots you have a function n(j). Think of n(j) as piecewise constant. There are two sequences: a threshold k_{n(j)}, and an interval width \delta_{n(j)}.

  1. Take the sample mean \hat{x}_{n(j)} and look at a interval of width 2 \delta_{n(j)} centered on it. Note that this makes the same decision for each j until n(j) changes.
  2. Given an enumeration of the set S, find the smallest i such that r_i \in [\hat{x} - \delta_{n(j)}, \hat{x} + \delta_{n(j)}].
  3. I there is an i < k_{n(j)} such that r_i \in [\hat{x} - \delta_{n(j)}, \hat{x} + \delta_{n(j)}] then declare p = r_i, otherwise declare p \notin S

    4. .

The last thing to do is pick all of these scalings. This is done in the paper (I won’t put it here), but the key thing to use is the law of the iterated logarithm (LIL), which I never really had a proper appreciation for prior to this. For \epsilon > 0,

| \hat{x}_n - p | \le (1 + \epsilon) (2 p (1 - p) \sqrt{ \frac{\log \log n}{n} })

for all but finitely many values of n. This gets used to set the interval width \delta_{n(j)}.

The cool thing to me about this paper is that it’s an example of “letting the hypothesis class grow with the data.” We’re trying to guess if the coin parameter p is rational and if so, which rational. But we can only apprehend a set of hypotheses commensurate with the data we have, so the threshold k_{n(j)} limits the “complexity” of the hypotheses we are willing to consider at time j. The LIL sets the threshold for us so that we don’t make too many errors.

There are lots of little extensions and discussions about the rationality of physical constants, testing for rationality by revealing digits one by one, and other fun ideas. It’s worth a skim for some of the readers of this blog, I’m sure. A miscellaneous last point : Blackwell suggested a Bayesian method for doing this (mentioned in the paper) using martingale arguments.

The history of the martingale

Posted on by

The other day I found myself wondering “so what does the word martingale come from?” A short time on Google later, I came across this paper from Journal Electronique d’Histoire des Probabilités et de la Statistique, which had a special issue on The Splendors and Miseries of Martingales (Splendeurs et misères des martingales):

The Origins of the Word “Martingale”
Roger Mansuy
(earlier version : “Histoire de martingales” in Mathématiques & Sciences Humaines/Mathematical Social Sciences, 43th year, no. 169, 2005(1), pp. 105–113.)

It’s 10 pages and worth a read just for fun. Some of the fun facts:

  • Doob is the one who really made the name popular (in addition to proving many fundamental results). He got the name from a thesis by Ville.
  • A martingale is the name for a Y-shaped strap used in a harness — it runs along the horse’s chest and then splits up the middle to join the saddle.
  • A martingale is a name for a betting strategy (usually we think of doubling bets) but it’s not clear which one from the historical record.
  • “To play the martingale is to always bet all that was lost” (dictionary of the Acad ́emie Fran ̧caise, 4th ed.) — there are earlier dictionary definitions too, to 1750.
  • “A very slim trail seems to indicate a derivation of the word from the Provençal expression jouga a la martegalo, which means ‘to play in an absurd and incomprehensible way’.” Apparently Provençal is also the origin of Baccarat.
  • So what is martegalo? It might refer to a place called Martigues, whose residents are supposedly a bit naïve.
  • “Martingale pants” are from Martigues, and have, according to Rabelais, “a drawbridge on the ass that makes excretion easier.”
  • There’s a woman in the 17th century who called herself La Martingale and who made a number of prophetic predictions.
  • There were sailors called martégaux who gave their name to a rope called a martegalo used on sailboats. Perhaps this is where the horse connection comes in?
  • Apparently “martingale” is also vernacular for “prostitute,” but the etymology for that usage is not well-documented.

All in all, perhaps this essay ends up raising more questions than it answers, but I certainly had no idea that there was this much to be unearthed behind a simple word.

Truth in surveying

Posted on by

A few weeks ago I attended Scott Kominers‘s class on Market Design. They were talking about mechanism design and differential privacy so I felt like it would be fun to attend that session. In the class Scott mentioned some interesting work by Nicholas Lambert and Yoav Shoham on Truthful Surveys that appeared at WINE 2008. There’s also some recent work by Aaron Roth and Grant Schoenebeck up on ArXiV.

In Lambert and Shoham’s set up, the opinion distribution of a population is given by some CDF F(x) (with a density) on the unit interval [0,1]. We can think of x as a level of approval (say of a politician) and F(x) as the proportion of the population which has approval less than x. A surveyor selects n agents \{x_i\} i.i.d. from F and asks them to report their opinion. They can report anything they like, however, so they will report \{r_i\}. In order to incentivize them, the surveyor will issue a payment \Pi_i( r_1, \ldots, r_n ) to each agent i. How should we structure the payments to incentivize truthful reporting? In particular, can we make a mechanism in which being truthful is a Nash equilibrium (“accurate”) or the only Nash equilibrium (“strongly accurate”)?

Let A_i = |\{j : r_i r_j \}|. They propose partitioning the agents into k groups with \mathcal{G}(i) denoting the group of agent $i$, and \tilde{F}_i(x) as an unbiased estimator of F(x) that uses the points \{r_j : \mathcal{G}_j \ne \mathcal{G}_i \}. The payments are:

\Pi_i(\{r_j\}) = \frac{1}{|\mathcal{G}_i| - 1} \left[ A_i - B_i \right] + 2 \tilde{F}_i(r_i) - \frac{2}{|\mathcal{G}_i| - 1} \sum_{j \in \mathcal{G}_i \setminus \{i\} } \tilde{F}_j(r_j)

This mechanism is accurate and also permutation-invariant with respect to the agents (“anonymous”) and the sum of the payments is 0 (“budget-balanced”).

This is an instance of a more general mechanism for truthfully inducing samples from a collection of distributions that are known — each agent has a distribution F_i and you want to get their sample of that distribution. Here what they do is replace the known distributions with empirical estimates, in a sense. Why is this only accurate and not strongly accurate? It is possible that the agents could collude and pick a different common distribution G and report values from that. Essentially, each group has an incentive to report from the same distribution and then globally the optimal thing is for all the groups to report from the same distribution, but that distribution need not be F if there is global collusion. How do we get around this issue? If there is a set of “trusted” agents \mathcal{T}, then the estimators in the payment model can be built using the trusted data and the remaining untrusted agents can be put in a single group whose optimal strategy is now to follow the trusted agents. That mechanism is strongly accurate. In a sense the trusted agents cause the population to “gel” under this payment strategy.

It seems that Roth and Schoenbeck are not aware of Lambert and Shoham’s work, or it is sufficiently unrelated (they certainly don’t cite it). They also look at truth in surveying from a mechanism design perspective. Their model is somewhat more involved (an has Bayesian bits), but may be of interest to readers who like auction design.

CISS 2012 : day 1

Posted on by

I’m at CISS right now on the magnolia-filled Princeton campus. The last time I came here was in 2008, when I was trying to graduate and was horribly ill, so this year was already a marked improvement. CISS bears some similarities to Allerton — there are several invited sessions in which the talks are a little longer than the submitted sessions. However, the session organizers get to schedule the entire morning or afternoon (3 hours) as they see fit, so hopping between sessions is not usually possible. I actually find this more relaxing — I know where I’m going to be for the afternoon, so I just settle down there instead of watching the clock so I don’t miss talk X in the other session.

Because there are these invited slots, I’ve begun to realize that I’ve seen some of the material before in other venues such as ITA. This is actually a good thing — in general, I’ve begun to realized that I have to see things 3 times for me to wrap my brain around them.

In the morning I went to Wojciech Szpankowski‘s session on the Science of Information, a sort of showcase for the new multi-university NSF Center. Peter Shor gave an overview of quantum information theory, ending with comments on the additivity conjecture. William Bialek discussed how improvements in array sensors for multi-neuron recording and other measurement technologies are allowing experimental verification of some theoretical/statistical approaches to neuroscience and communication in biological systems. In particular, he discussed an interesting example of how segmentation appears in the embryonic development of fruit flies and how they can track the propagation of chemical markers during development.

David Tse gave a slightly longer version of his ITA talk (with on DNA sequencing with more of the proof details. It’s a cute version of the genome assembly problem but I am not entirely sure what it tells us about the host of other questions biologists have about this data. I’m trying to wrestle with some short-read sequencing data to understand it (and learning some Bioconductor in the process), and the real data is pretty darn messy.

Madhu Sudan talked about his work with Brendan Juba (and now Oded Goldreich) on Semantic Communication — it’s mostly trying to come up with definitions of what it means to communicate meaning using computer science, and somehow feels like some of these early papers in Information and Control which tried to mathematize linguistics or other fields. This is the magical 3rd time I’ve seen this material, so maybe it’s starting to make sense to me.

Andrea Goldsmith gave a whirlwind tour of the work in backing away from asymptotic studies in information theory, and how insights we get from asymptotic analyses often don’t translate into the finite parameter regime. This is of a piece with her stand a few years ago on cross-layer design. High SNR assumptions in MIMO and relaying imply that certain tradeoffs (such diversity-multiplexing) or certain protocols (such as amplify-and forward) are fundamental but at moderate SNR the optimal strategies are different or unknown. Infinite blocklengths are the bread and butter of information theory but now there are more results on what we can do with finite blocklength. She ended with some comments on infinite processing power and trying to consider transmit and processing power jointly, which caused some debate in the audience.

Alas, I missed Tsachy Weissmann‘s talk, but at least I saw it at ITA? Perhaps I will get to see it two more times in the future!

In the afternoon I went to the large alphabets session which was organized by Aaron Wagner. Unfortunately, Aaron couldn’t make it so I ended up chairing the session. Venkat Chandrasekaran didn’t really talk about large alphabets, but instead about estimating high dimensional covariance matrices when you have symmetry assumptions on the matrix. These are represented by the invariance of the true covariance under actions of a subgroup of the symmetric group — taking these into account can greatly improve sample complexity bounds. Mesrob Ohanessian talked about his canonical estimation framework for large alphabet problems and summarized a lot of other work before (too briefly!) mentioning his own work on the consistency of estimators under some assumptions on the generating distribution.

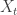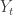Prasad Santhanam talked about the insurance problem that he worked on with Venkat Anantharam, and I finally understood it a bit better. Suppose you are observing i.i.d. samples X_t from a distribution P on \mathbb{R}^{+} that represent losses paid out by an insurer. The insurer gets to observe the losses for a while and then has to start setting premiums Y_t. The question is this : when can we guarantee that 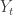Y_t remains bounded and \mathbb{P}( Y_t > X_t \forall t ) > 1 - \eta? In this case we would say the distribution is insurable.

To round out the session, Wojciech Szpankowski gave a talk on analytic approaches to bounding minimax redundancy under different scaling assumptions on the alphabet and sample sizes. There was a fair bit of generatingfunctionology and Lambert W-functions. The end part of the talk was on scaling when you know part of the distribution exactly (perhaps through offline simulation or training) but then there is part which is unknown. The last talk was by Greg Valiant, who talked about his papers with Paul Valiant on estimating properties of distributions on n elements using only \Theta(n/\log n) samples. It was a variant of the talk he gave at Banff, but I think I understood the lower bound CLT results a bit better (using Stein’s Method).

I am not sure how much blogging I will do about the rest of the conference, but probably another post or two. Despite the drizzle, the spring is rather beautiful here — la joie du printemps.

Avoidance Coupling

Posted on by

I took a read through this fun paper that appeared on ArXiV a few months ago:

Avoidance Coupling
Omer Angel, Alexander E. Holroyd, James Martin, David B. Wilson, Peter Winkler
arXiv:1112.3304v1 [math.PR]

Typically when you think of coupling arguments, you want to create two (or more) copies of a Markov chain such that they meet up quickly. A coupling of Markov chains with transition matrix P is a sequence of pairs of \{(U_t, V_t)\} such that \{U_t\} and \{V_t\} are Markov chains with transition matrix P:

\mathbb{P}( U_{t+1} = j | U_t = i, V_t = i') = P(i,j)
\mathbb{P}( V_{t+1} = j' | U_t = i, V_t = i') = P(i', j')

Note that the two chains need not be independent! The idea is that we start \{U_t\} and \{V_t\} at different initial positions and when they “meet” we make them move together. Once they meet, the decisions from random mappings are the same for both chains. The coupling time is T_c = \min \{t : U_t = V_t \}. Coupling is used to show fast mixing of Markov chains via theorems like the following, which says that the difference between the distribution of the chain started at time i and the chain started at time i' at time t is upper bounded by the probability of coupling:

Theorem. Let \{ (U_t,V_t) \} be a coupling with U_0 = i and V_0 = i'. Then

\| P^t(i,\cdot) - P^t(i',\cdot) \|_{\mathrm{TV}} \le \mathbb{P}_{(U,V)}\left( T_c > t \right)

This paper takes an entirely different tack — sometimes you want to start off a bunch of copies of the chain such that they never meet up. This could happen if you are trying to cover more of the space. So you want to arrange a coupling such that the coupling time is huge. There’s a bit of a definitional issue regarding when you declare that two walkers collide (what if they swap places) but they just say “multiple walkers are assumed to take turns in a fixed cyclic order, and again, a collision is deemed to occur exactly if a walker moves to a vertex currently occupied by another. We call a coupling that forbids collisions an avoidance coupling.”

There are a number of results in the paper, but the simplest one to describe is for two walkers on a complete graph K_n (or the complete graph with loops K_n^{\ast}.

Theorem 4.1. For any composite n = ab, where a,b > 1, there exist Markovian avoidance couplings for two walkers on K_n and on K_n^{\ast}.

How do they do this? They partition n into b clusters \{S_i\} of size a. Let’s call the walkers Alice and Bob. Suppose Alice and Bob are in the same cluster and it’s Bob’s turn to move. Then he chooses uniformly among the vertices in another cluster. If they are in different clusters, he moves uniformly to a vertex in his own cluster (other than his own). Now when it’s Alice’s turn to move, she is always in a different cluster than Bob. She picks a vertex uniformly in Bob’s cluster (other than Bob’s) with probability \frac{a(b-1)}{ab - 1} and a vertex in her own cluster (other than her own) with probability \frac{a - 1}{ab - 1}.

So let’s look at Bob’s distribution. The chance that he moves to a particular vertex outside his current cluster is the chance that Alice moved into his cluster times the uniform probability of choosing something outside his cluster:
\frac{a(b-1)}{ab - 1} \times \frac{a (b-1)} = \frac{1}{ab - 1}
The chance that he moves to a vertex inside his own cluster is likewise
\frac{a - 1}{ab - 1} \times \frac{1}{a-1} = \frac{1}{ab - 1}
So the marginal transitions of Bob are the same as a uniform random walk.

For Alice’s distribution we look at the time reversal of the chain. In this case, Alice’s reverse distribution is Bob’s forward distribution and vice versa, so Alice also looks like a uniform random walk.

There are a number of additional results in the paper, such as:

Theorem 7.1. There exists a Markovian avoidance coupling of k walkers on K_n^{\ast} for any k \le n/(8 log_2 n), and on K_n for any k \le n/(56 log_2 n)$.

Theorem 8.1. No avoidance coupling is possible for n - 1 walkers on K_n^{\ast} , for n \ge 4.

In addition there are a ton of open questions at the end which are quite interesting. I didn’t mention it here, but there are also interesting questions of the entropy of the coupling — lower entropy implies easier simulation, in a sense.

Products of random stochastic matrices

Posted on by

As I mentioned, Behrouz Touri gave a really great presentation at ITA on some of his work with Angelia Nedić on products of stochastic matrices, some of which was in this paper on ArXiV. The setup of the paper is relatively straightforward — we have a sequence of independent random matrices \{W(k)\}, each of which is row-stochastic almost surely, and we want to know when the product \lim_{k \to \infty} W(k) W(k-1) \cdots W(t_0) converges almost surely. The main result is that if the chain is balanced and strongly aperiodic, then the limit is a random stochastic matrix such that the rows in the same connected component of the infinite flow graph are equal.

Recall that for a chain W a lazy version of the chain is \alpha W + (1 - \alpha) I. Laziness helps avoid periodicity by letting the chain be “stuck” with probability (1 - \alpha). Strongly aperiodic means that there is a \gamma \in (0,1] such that \mathbb{E}[ W_{ii}(k) W_{ij}(k) ] \ge \gamma \mathbb{E}[ W_{ij}(k) ]. Basically this is a sort of “expected laziness condition” which says that there is enough self-transition probability to avoid some sort of weak periodicity in the chain.

Consider a cut of the chain into a set of states S and a set \bar{S}. A chain is balanced if there is an \alpha > 0 such that for all cuts (S,\bar{S}), we have \mathbb{E}[ W_{S \bar{S}}(k) ] \ge \alpha \mathbb{E}[ W_{\bar{S} S}(k) ]. So this is saying that at each time, the flow out of S is commensurate with the flow into S.

The infinite flow graph has the same vertex set as the original chain, but with edge (i,j) existing only if \sum_{k} W_{ij}(k) + W_{ji}(k) = \infty. That is, the edge has to exist infinitely often in the graph.

So to add it all up, the well-behaved independent products of stochastic matrices that converge are those which don’t behave badly over time — for each time k, they don’t shift around the mass too much and they are not too periodic. Basically, they don’t become volatile and cyclical, which sounds perfectly reasonable. So how does he prove it?

The first part is to connect the problem with a dynamic system whose state x(k+1) = W(k+1) x(k) and look to see if the state converges in the limit. The next part uses a connection to absolute probability processes, which were used by Kolmogorov in 1936. A random vector process \pi(k) is an absolute probability process for \{W(k)\} if it is adapted to the same filtration as the chain, it’s stochastic almost surely, and

\mathbb{E}[ \pi(k+1) W(k+1) | \mathcal{F}_k ] = \pi(k)

Kolmogorov showed that for a deterministic sequence of stochastic matrices there is always an deterministic absolute probability process, so for independent chains we can always find a random absolute probability process. Using this, Touri and Nedić define a class of comparison functions which are super-martingales for each $\latex x(0)$ and have a limit. By choosing a particular comparison function they can get a version of the main result. It’s a nicely written paper and worth a skim if you’re interested in these things (as I am).