This is the penultimate post on papers I saw at ISIT 2009 that I thought were interesting and on which I took some notes. I think I’m getting lazier and lazier with the note taking — I went to lots more talks than these, but I’m only writing about a random subset.
Existence and Construction of Capacity-Achieving Network Codes for Distributed Storage
Yunnan Wu
This paper looked at the distributed storage problem using the framework of network coding that Alex has worked on. The basic idea is that you have a bunch of drives redundantly storing some information (say n drives and you can query any k to reconstruct the data). You want to make it so that if any drive fails, it can be replaced by a new drive so that the new drive doesn’t have to download too much data to maintain the “k out of n” property. The problem can be translated into a network code on an infinite graph. This paper talked about how to achieve the optimal tradeoff between the bandwidth needed to repair the code and the storage efficiency/redundancy. The key thing is that even though the network graph is infinite, the network code can be constructed over a field whose size only depends on the number of active disks. Schwartz-Zippel reared its head again in the proof…
Achievability Results for Statistical Learning under Communication Constraints
Maxim Raginsky
This talk was on how to learn a classifier when the data-label pairs 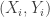 must be compressed. Max talked about two different scenarios, one in which you can use
must be compressed. Max talked about two different scenarios, one in which you can use 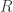 bits per pair, and the other in which only the labels
bits per pair, and the other in which only the labels 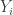 must be sent. He defined a rate-distortion-like function where the generalization error the classifier played the role of the distortion. In the first case it’s easier for the encoder to learn the classifier itself and send the classifier over — this takes 0 bits per sample, asympotically, and incurs no extra generalization error. In the second case he uses a kind of Wyner-Ziv-like scheme which is a bit more involved. Compression is not a thing many machine learning folks think about, so I think there’s a lot of interesting stuff in this direction.
must be sent. He defined a rate-distortion-like function where the generalization error the classifier played the role of the distortion. In the first case it’s easier for the encoder to learn the classifier itself and send the classifier over — this takes 0 bits per sample, asympotically, and incurs no extra generalization error. In the second case he uses a kind of Wyner-Ziv-like scheme which is a bit more involved. Compression is not a thing many machine learning folks think about, so I think there’s a lot of interesting stuff in this direction.
On Feedback in Network Source Coding
Mayank Bakshi, Michelle Effros
This paper was about how feedback can help in distributed source coding. In some lossless and lossy problems, feedback can strictly increase the rate region. Some of these problems took the form of “helper” scenarios where the decoder wants one of the sources but gets coded side information from another source. They show that this scenario holds more generally, and so feedback helps in general in network source coding.
Feedback Communication over Individual Channels
Power Adaptive Feedback Communication over an Additive Individual Noise Sequence Channel
Yuval Lomnitz, Meir Feder
These talks were near and dear to my heart since they dealt with coding over channels which are basically unknown. The basic idea is that you know only  and
and  , the inputs and outputs of the channel. The trick is then to define a corresponding “achievable rate.” They define an empirical mutual information and show that it is asymptotically achievable under some circumstances. The scheme is based on random coding plus maximum mutual information (MMI) decoding. When feedback is present they can do some rateless coding. There’s a full version on ArXiV.
, the inputs and outputs of the channel. The trick is then to define a corresponding “achievable rate.” They define an empirical mutual information and show that it is asymptotically achievable under some circumstances. The scheme is based on random coding plus maximum mutual information (MMI) decoding. When feedback is present they can do some rateless coding. There’s a full version on ArXiV.
Upper Bounds to Error Probability with Feedback
Barış Nakiboğlu, Lizhong Zheng
Baris gave a nice talk on his approach to modifying the Gallager exponent bounds to the case when feedback is available. The encoder constantly adapts to force the decoder into a decision. The upper bound is based on a one-step/channel-use reduction to show an exponentially decaying error probability. One nice thing he mentioned is that at rates below capacity we can get a better error exponent by not using the capacity-achieving input distribution. Even though I read the paper and Barış explained it to me very patiently, I still don’t quite get what is going on here. That’s probably because I never really worked on error exponents…
?
to give the guarantee. To do the minimization we need to turn to convex optimization tools (which might be a subject for another post — numerically minimizing the KL divergence requires choosing your solving algorithm carefully).


