Tag Archives: machine learning

Domingos on what you should know about machine learning

Posted on by

Dhruv Batra forwarded this Communications of the ACM article by Pedro Domingos, entitled “A Few Useful Things to Know about Machine Learning” [free version] The main point from the abstract is:

However, developing successful machine learning applications requires a substantial amount of “black art” that is hard to find in textbooks. This article summarizes twelve key lessons that machine learning researchers and practitioners have learned. These include pitfalls to avoid, important issues to focus on, and answers to common questions.

The article focuses on the classification problem to illustrate these “key lessons.” It’s well-worth reading, especially for people who don’t work on machine learning because it explains a number of important issues.

  1. It illustrates the gap between what the theory/research works on and the nitty-gritty of applying these algorithms to real data.
  2. It gives people who want to implement an ML method important fundamental questions to ask before starting : how do I represent my data? How do I evaluate performance? How do I do things efficiently? These have to get squared away first.
  3. Domain knowledge and feature engineering are the keys to success.

Since I’m guessing there are 2 machine learners who read this blog, go read it (unless you are one of my friends who doesn’t care about all of these technical posts).

Linkage

Posted on by

Via Amber, a collection of grassroots feminist political posters from India.

Via John, some fun investigations on how 355/113 is an amazingly good approximation to \pi. Also related are the Stern-Brocot trees, which can give continued fraction expansions.

I had missed this speech by a 10 year old on gay marriage when it happened (I was in India), but it’s pretty heartwarming. For more background on how the principal originally deemed the story “inappropriate.”

What is a Bayesian?

Unrelatedly, ML Hipster — tight bounds and tight jeans.

ArXiV notes : July 2012 part 1

Posted on by

I usually tag things from ArXiV that I want to skim later, so I figured I would post the ones I found interesting in the last month or so. Some of them may deserve their own post later. Jet lag is not letting me take the nap I need right now so I figured I’d post it before conking out.

Convergence Rates for Differentially Private Statistical Estimation
K. Chaudhuri and D. Hsu
ArXiV 1206.6395
This paper is about estimation under privacy constraints. In differential privacy there are a fair number of constraints with regards to the data being well behaved — typical assumptions include boundedness, for example. One way around this is to move to a relaxed notion of privacy known as (\alpha,\delta)-differential privacy, but what this paper shows is that for the stricter \alpha-differential privacy definition, statistical estimation is governed by the gross error sensitivity (GES) of the estimator.

The Greedy Miser: Learning under Test-time Budgets
Z. Xu, K. Weinberger, and O. Chapelle
ArXiV 1206.6451
This paper is about incorporating the cost of extracting features in classification or regression. For a data point \mathbf{x}_i \in \mathbb{R}^d, the feature \alpha costs c_{\alpha} to compute and there is a total budget for the computation. The main approach is to minimize a linear combination of the loss and the cost iteratively, where each iteration consists of building a regression tree.

Sequential detection of multiple change points in networks: a graphical model approach
A.A. Amini and X. Nguyen
ArXiV 1207.1687
This looks at the change point detection problem in the network setting, where each of d nodes in a network has a change point \lambda_j. Data is observed on vertices and edges and nodes have to pass messages on the graph. There’s a prior distribution on the change point times and after observing the data the nodes can use message passing to do some belief propagation to estimate the posterior distribution and define a stopping time. This turns out to be asymptotically optimal, in that the expected delay in detecting the change point is achieved.

The Price of Privacy in Untrusted Recommendation Engines
S. Bannerjee, N. Hegde, and L. Massoulié
ArXiV 1207.3269
This studies the effect on recommendations engines of individuals masking their data due to privacy concerns. The technical issues are the the dimension is high and each user only has a small amount of data to control (e.g. the movies that they rented or have seen). The question is one of sample complexity — how many users do we need to cluster successfully. If users are not so sparse, they can achieve the Fano lower bound (order-wise) using a sketch and spectral techniques, but the dependence is like N \log N, where $N$ is the number of items (e.g. movies). It’s worse if the users are sparse — the scaling is with N^2, which is also achievable in some settings. The analysis approach using Fano is analogous to the “information leakage” connections with differential privacy.

Surrogate Losses in Passive and Active Learning
S. Hanneke and L. Yang
ArXiV 1207.3772
This paper looks at how to use surrogate losses (which are computationally tractable) in active learning problems. “We take as our starting point that we have already committed to use a given surrogate loss, and we restrict our attention to just those scenarios in which this heuristic actually does work. We are then interested in how best to make use of the surrogate loss toward the goal of producing a classifier with relatively small error rate.” The central insight in their algorithm is that by taking into account the fact that the “real loss” is (say) the 0-1 loss, then for the purposes of active learning, one only really needs to get the sign right and not the magnitude. So the process will minimize the real loss but not necessarily the surrogate.

If at first you don’t succeed, normalize, normalize again

Posted on by

My ex-groupmate and fellow Uni High graduate Galen Reeves told me about a paper a few weeks ago when I visited him at Stanford:

Successive Normalization of Rectangular Arrays
Richard A. Olshen and Bala Rajaratnam
The Annals of Statistics 38(3), pp.1369-1664, 2010

Apparently, however, the arguments in the paper are not quite correct [1], and they recently uploaded a correction to ArXiV.

This paper looks at the effect of a very common preprocessing step used to transform an n \times k data matrix \mathbf{X} into a form acceptable for statistical or machine learning algorithms that assume things like zero-mean or bounded vectors. Here n may represent the number of individuals, and k the number of features, for example. Or the data may come from a DNA microarray (their motivating example). This preprocessing is often done without much theoretical justification — the mathematical equivalence of tossing spilled salt over your shoulder. This paper looks at the limiting process of standardizing rows and then columns and then rows and then columns again and again. 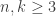They further need that n,k \ge 3. “Readers will see that the process and perhaps especially the mathematics that underlies it are not as simple as we had hoped they would be.”

So what exactly is the preprocessing? I am going to describe things in pseudocode (too lazy to do real code, sorry). Given a data matrix X[i,j] they look at

for i = 1:n { X[i,1:k] = X[i,1:k] - sum(X[i,1:k]) }
for j = 1:k { X[1:n,j] = X[l:n,j] - sum(X[1:n,j]) }

They call the first a “row mean polish” and the second a “column mean polish.” They show this converges in one step.

But what about standardizing? The more complicated polishing procedure looks like this:

for i = 1:n {
mu = sum(X[i,1:k])
sigma = sqrt( sum( (X[i,1:k] - mu)^2 ) )
X[i,1:k] = (X[i,1:k] - mu)/sigma
}
for j = 1:k {
mu = sum(X[1:n,j])
sigma = sqrt( sum( (X[1:n,j] - mu)^2 ) )
X[1:n,j] = (X[1:n,j] - mu)/sigma
}

This standardizes rows first, and then columns (or “lather” and “rinse,” since we are going to “repeat”). They call this Efron‘s algorithm because he told them about it. So what happens if we repeat these two steps over and over again on a matrix with i.i.d. entries from some continuous distribution?

Theorem 4.1 Efron’s algorithm converges almost surely for X on a Borel set of entries with complement a set of Lebesgue measure 0.

So what does it look like in practice? How fast is this convergence? Empirically, it looks exponential, and they have some theoretical guarantees in the paper, kind of hidden in the discussion. The proofs are not terribly ornate but are tricky, and I don’t quite get all the details myself, but I figured readers of this blog would certainly be interested in this cute result.

[1] A fun quote from the paper “Theorem 4.1 of [2] is false. A claimed backwards martingale is NOT. Fortunately, all that seems damaged by the mistake is pride. Much is true.” I really liked this.

Differentially Private ERM

Posted on by

Right after Memorial Day, I submitted a paper with Kamalika Chaudhuri and Claire Monteleoni to the Journal of Machine Learning Research on differential privacy and empirical risk minimization. This work looks at how to learn a classifier from training data in such a way that an adversary with access to the classifier and full knowledge of all but one of the training data points would still have a difficult time inferring the values of the last data point.

Ben Rubenstein has a nice post on the differential privacy model, and Adam Smith has more to say on sample secrecy. Adam and his colleagues (Dan Kifer and Abhradeep Guha Thakurta) gave us useful feedback on an earlier draft, which prompted me to learn some new facts about matrix perturbations, symmetric functions, and eigenvalues. Perhaps I’ll blog about this a bit more in the future, but I seem to be going in fits and starts here, so I don’t want to promise anything.

On a related note, ArXiV has dramatically changed its interface for submissions, and it is soooooo much better than before.

Talk at USC Wednesday

Posted on by

In case you’re at USC or in the area, I’m giving a talk tomorrow there on some of the work I’ve been doing with Kamalika Chaudhuri (whose website seems to have moved) and Claire Monteleoni on privacy-preserving machine learning.

Learning from sensitive data – balancing accuracy and privacy

Wednesday, March 24th, 2010
2:00pm-3:00pm
EEB 248

The advent of electronic databases has made it possible to perform data mining and statistical analyses of populations with applications from public health to infrastructure planning. However, the analysis of individuals’ data, even for aggregate statistics, raises questions of privacy which in turn require formal mathematical analysis. A recent measure called differential privacy provides a rigorous statistical privacy guarantee to every individual in the database. We develop privacy-preserving support vector machines (SVMs) that give an improved tradeoff between misclassification error and the privacy level. Our techniques are an application of a more general method for ensuring privacy in convex optimization problems.

Joint work with Kamalika Chaudhuri (UCSD) and Claire Monteleoni (Columbia)

Privacy Workshop at IPAM

Posted on by

I’m at the Institute for Pure and Applied Math at a workshop on Statistical and Learning-Theoretic Challenges in Data Privacy. It’s a rather diverse group of computer scientists, statisticians, medical informatics, and policy researchers, and I feel a bit like I’m the only electrical engineer here. It’sa been pretty educational in the “learning about new problems” way, but I think by the time Friday morning rolls around I’ll be suffering from information overload. The nice thing is that the slides are posted online so I can refresh my memory when I get back. There’s also a poster session for some more recent results.

Most of the speakers have been talking about either (a) applications of the differential privacy model to some problems (e.g. data release, function computation, classification, PAC-learning, auctions, or Google’s MapReduce, the Census Bureau’s OnTheMap, and PINQ)or (b) areas in which privacy is a real problem (hospital discharge data and the dangers of re-identification, genome-wide association studies (GWAS), query logs from search engines, or (c) bridges between fields and their privacy definitions and models.

I’ve just started working in this area, so I’m still processing things (the talks range from high level to technical, and I often lack the background to understand fully what’s going on). I might blog a bit more about it as things come up.

ArXiV is down

Posted on by

I got the following from ArXiV today:

Submissions to arXiv have been disabled for maintenance. arXiv’s database is down for maintenance. It is still possible to browse, view and search papers that have already been announced but submissions and replacements disabled, as are the functions to add cross listings and journal references.

So I guess I’ll have to wait to post our new submission, “Privacy constraints in regularized convex optimization,” until the system comes back up.

In the meantime, I’ll blog a bit about ISIT!