I am trying to figure out a rather simple question but I’m sure it’s known already. Suppose I have a the minimizer of the following regularized optimization:
Here is a continuous convex function of
. Is
a continuous function of
? I want to say yes, but maybe I need more assumptions on
.
I believe the answer is yes, and I think a proof should not be hard. As in, you’re way more mathematical these days than I am, and I think I could prove it. Have you tried to work out a proof?
Actually, don’t you have to be a little more careful. The value of the regularization functional is definitely going to be a continuous function of lambda, but to talk about f* itself being continuous, do you need to talk about a distance norm on functions?
Exactly, so we can take the (say) RHKS norm on the difference of functions (which is like L2 I guess) and then ask for continuity with respect to that. The approaches I’ve been taking have been a bit simple so far and my optimization theory/functional analysis knowledge is a bit rusty.
I knew this post would get you interested :-)
Lorenzo Rosasco (lrosasco@mit.edu) will definitely know the answer.
I’m pretty sure that if if L is continuous in L2 (or likely RKHS), that f* will be continuous in that as well.
Should lambda be positive and should script-F be a convex subset of R^n? If not, the existence of a unique f* is not guaranteed.
Sure,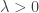 but I want to think of
but I want to think of 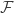 as a general Hilbert space (specifically a function space).
as a general Hilbert space (specifically a function space).
My optimization background is also rusty, but I think the following argument works:
Suppose not. This means there exists a sequence
lambda_1, lambda_2, ….
each positive, converging to
lambda > 0
such that
O_1(f_1^*), O_2(f_2^*), ….
are each at least epsilon>0 away from
O(f^*).
Here I use: O_i for the objective function with lambda_i, f_i^* for the minimizer of O_i, O for the objective function with lambda, f^* for the minimizer with lambda.
So we have
|O_i(f_i^*) – O(f)| > epsilon
for all i.
Now since
lim_i O_i(f) = O(f)
this means there exists some positive
epsilon’ such that for large enough i
|O_i(f_i^*) – O_i(f)| > epsilon’
Now if for any i the term inside the
absolute value was positive, this would contradict the optimality of f_i^* for O_i!
So the term within the absolute value always has to be negative. Thus:
O_i(f) – O_i(f_i^*) > epsilon’.
From this, we will try to contradict the optimality of f for O.
Observe that the previous equation immediately implies that
||f_i^*||^2 cannot go infinity, because then O_i(f)=infinity. So: ||f_i^*||^2
stays bounded.
This means that for i large enough,
O(f) – O(f_i^*) > epsilon”
for some positive epsilon”, contradicting
the optimality of f for O.
So this shows the objective value at the optimum is a continuous function of , but I think the function $\latex f^{\ast}$ is a continuous function of
, but I think the function $\latex f^{\ast}$ is a continuous function of  as well…
as well…
Oops – somehow I missed the arg in front of the min. Sorry.
To show that you have to use that your regularized objective function is not just convex but “strongly convex” – this is not the same as “strictly convex.” For definition see
you have to use that your regularized objective function is not just convex but “strongly convex” – this is not the same as “strictly convex.” For definition see
http://books.google.com/books?id=GrlRqY9EVzgC&pg=PA290&vq=strongly+convex&dq=Numerical+analysis+and+optimization&source=gbs_search_s&cad=0
In the above link, Theore 9.2.6 (a page or so down) implies that if does not converge to $f_i$, then the objective functions will not converge either.
does not converge to $f_i$, then the objective functions will not converge either.
er, that should be “if does not converge to
does not converge to 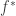 ”
”
by the way, a previous button on your blog would be nice :)
I see! Thanks for this reference and the argument!
urgh. a preview button is what i meant to say.
I should look into that… I didn’t even know that there was comment threading until yesterday!
Then again, maybe I should post more questions about things I don’t understand :-)
I think the answer is yes. First, f*(\lambda) is monotonically increasing (hopefully bounded if your functions are not too weird) with \lamda. Which means it is at least continuous everywhere (left limit = right limit, of course both exist because f*(\lambda) is monotonic ) except at most countable many points of \lambda.
Now suppose at a point \lambda, the function is NOT continuous, then for any sequence of increasing \lambda_i’s that is converging to \lambda from the left, f*(\lambda_i)’s are monotonically increasing and bounded, so you have a left limit here, similarly you have a right limit. Now if these two disagree, you have a gap between the two. At this point, you can go back to the original form of the thing and draw a contradiction.
PS: hope this all make sense, I have not opened a real analysis book for several years.